first-data-structure-algorithm

선형 배열
탐색
재귀
- 복잡도
- 예제
재귀 응용
- 예제
알고리즘의 복잡도
- 설명
연결 리스트
Stack
큐
트리
힙(heap)
- Maxheap
Link

선형 배열

정렬된 리스트에 원소 삽입

def solution(L, x):
    if x > max(L): 
        L.append(x)
    elif x < min(L): 
        L.insert(0, x)
    else:
        for i in range(len(L)):
            if L[i] >= x:
                t = i
                break
        L.insert(t, x) 

    return L

def solution(L, x):
    for idx, num in enumerate(L):
        if num > x:
            L.insert(idx,x)
            break

        if L[-1] < x:
            L.append(x)
        else:
            pass

     return L

리스트에서 원소 찾아내기

def solution(L, x):
    answer = []
    if x not in L:
        answer.append(-1)
    else:
        for i in range(len(L)):
            if L[i] == x:
                answer.append(i)        
    return answer

def solution(L, x):
    answer = []
    if x not in L:
        answer.append(-1)
    else:
        for i, v in enumerate(L):
            if v == x:
                answer.append(i)
    return answer

탐색

def solution(L, x):
    lower = 0
    upper = len(L) - 1
    idx = -1
    while lower <= upper:
        middle = (lower + upper) // 2
        if L[middle] == x:
            idx = middle
            break
        elif L[middle] < x:
            lower = middle + 1
        else:
            upper = middle - 1
    return idx

이진 탐색 O(log n)
sorted()
- 내장 함수
- 정렬된 새로운 리스트 얻어냄(오름차순)

>>> sorted([5, 2, 3, 1, 4])
[1, 2, 3, 4, 5]

sort()
- 리스트의 메서드
- 해당 리스트를 정렬함

>>> a = [5, 2, 3, 1, 4]
>>> a.sort()
>>> a
[1, 2, 3, 4, 5]

reverse = True 정렬 순서 반대로

L2 = sorted(L, reverse = True)

길이순

L = ['abcd', 'xyz', 'spam']
sorted(L, key=lambda x: len(x))

L = [{'name': 'John', 'score': 83},.. ]

L.sort(key = lambda x:x['name'])
# 알파벳 순으로 정렬

재귀

sum(n) = sum(n - 1) + n

복잡도

O(n)
recusive version vs iterative version
복잡도는 같지만 효율적 측면에서 recursive가 떨어짐. 함수 호출 등의 과정 때문?

예제

def what(n):
    if n <= 1:
        return 1
    else:
        return n * what(n - 1)

fibonacci

# recursive version
def solution(x):
    if x == 0:
        return 0;
    elif x == 1:
        return 1;
    elif x < 0:
        return -1;
    else:
        return solution(x-1) + solution(x-2)

# iterative version
def solution(x):
    answer = 0
    fa = 0
    fb = 1
    while x > 0:
        x -= 1
        fa, fb = fb, fa+fb
        answer = fa
    return answer

재귀 응용

예제

조합의 수 계산
- n개의 서로 다른 원소에서 m개를 택하는 경우의 수

from math import factorial as f

def combi(n, m):
    return f(n) / (f(m) * f(n - m))

def combi(n, m):
    if n == m:
        return 1
    elif m == 0:
        return 1
    else:
        return combi(n - 1, m) + combi(n - 1, m - 1)

반복문보다 효율이 떨어지는 재귀. 그러나 사람이 직관적으로 이해하므로 쓸모 있을 떄가 있다.
- 하노이의 탑
- 트리구조
재귀적 이진탐색

def solution(L, x, l, u):
    if l > u:
        return -1
    mid = (l + u) // 2
    if x == L[mid]:
        return mid
    elif x < L[mid]
        return solution(L, x, l, mid - 1)
    else:
        return solution(L, x, mid + 1, u)

알고리즘의 복잡도

설명

시간 복잡도
- 문제의 크기와 이를 해결하는 데 걸리는 시간 사이의 관계
공간 복잡도
- 문제의 크기와 이를 해결하는 데 필요한 메모리 공간 사이의 관계
Big-O Notation
- 점근 표기법(asymptotic notation)의 하나
- 상수는 중요하지 않음
- 어떤 함수의 증가 양사을 다른 함수와의 비교로 표현(알고리즘의 복잡도를 표현할 때 흔히 쓰임)
- 예) 선형 시간 알고리즘 - O(n)
- 로그 시간 알고리즘 - O(log n)
  - n개의 크기 순으로 정렬된 수에서 특정 값을 찾기 위해 이진 탐색 알고리즘을 적용
- 이차 시간 알고리즘 - O(n제곱)
  - 삽입 정렬
- 병합 정렬 - O(nlog n) (merge sort)

연결 리스트

설명

장점
- 삽입, 삭제, 합치기 유연
단점
- 메모리 소모 크다
- k번째 찾아가는 데 배열보다 오래 걸린다
Linked List Node 구성
- Data
- Link(next)
  - 노드 내 데이터는 다른 구조로 이뤄질 수 있음 예) 문제열, 레코드, 다른 연결 리스트 등
기본적 연결 리스트
- Head (노드의 처음 값)
- Tail (노드의 마지막 값)
- of nodes: 3 (노드수)

시간 복잡도

특정 원소 지칭 - 배열 O(1), 연결 리스트 O(n)

예제

순회

class Node:
    def __init__(self, item):
        self.data = item
        self.next = None

class LinkedList:  # 연결 리스트 요소의 맨 앞이 헤드, 맨 끝은 테일
    def __init__(self):
        self.nodeCount = 0
        self.head = None
        self.tail = None

    def getAt(self, pos): # pos번째 노드를 찾아서 리턴
        if pos < 1 or pos > self.nodeCount:
            return Node
        i = 1 # 인덱스 1부터 시작

        curr = self.head
        while i < pos:
            curr = curr.next
            i += 1
        return curr
    
    def traverse(self):
        answer = []
        curr = self.head
        while curr != None:
            answer.append(curr.data)
            curr = curr.next
        return answer

삽입

원소 삽입
- pos가 가리키는 위치에 (1 <= pos <= nodeCount + 1)
- newNode를 삽입하고 성공/실패에 따라 True/False 리턴
- 복잡도
  - 맨 앞 삽입: O(1)
  - 중간 삽입: O(n)
  - 맨 끝 삽입 O(1) - Tail 덕분에
두 리스트의 연결
- concat

...
    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        if pos == 1:
            newNode.next = self.head
            self.head = newNode

        else:
            if pos == self.nodeCount + 1:
                prev = self.tail
            else:
                prev = self.getAt(pos - 1)
            newNode.next = prev.next
            prev.next = newNode

        if pos == self.nodeCount + 1:
            self.tail = newNode

        self.nodeCount += 1
        return True


    def getLength(self):
        return self.nodeCount


    def traverse(self):
        result = []
        curr = self.head
        while curr is not None:
            result.append(curr.data)
            curr = curr.next
        return result


    def concat(self, L):
        self.tail.next = L.head
        if L.tail:
            self.tail = L.tail
        self.nodeCount += L.nodeCount

삭제

원소의 삭제
- pos가 가리키는 위치의 (1 <= pos <= nodeCount)
- node를 삭제하고
- 그 node의 데이터를 리턴
- 복잡도
  - 맨 앞 삭제: O(1)
  - 중간 삭제: O(n)
  - 맨 끝 삭제: O(n)

...
    def popAt(self, pos):
        if 1 > pos or pos > self.nodeCount:
            raise IndexError
        
        curr = self.getAt(pos)

        if pos == 1 and pos == self.nodeCount:
            self.head = None
            self.tail = None
        elif pos == 1:
            self.head = self.getAt(pos + 1)
        else:
            prev = self.getAt(pos - 1)
            
            if self.nodeCount != pos:
                prev.next = self.getAt(pos + 1)
            else:
                prev.next = None
                self.tail = prev
        
        self.nodeCount = self.nodeCount - 1
        return curr.data
...

insertAfter, insertAt

삽입과 삭제 유연 장점 설려서
- 포지션을 수가 아니라 노드로, 주어진 노드 뒤에 삽입
  - 맨 앞에 dummy node 추가
    - self.head = Node(None)
  - index를 1이 아닌 0부터 시작

class Node: 
    def __init__(self, item):
        self.data = item
        self.next = None 

class LinkedList: 
    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = None
        self.head.next = self.tail

    def traverse(self):
        result = []
        curr = self.head
        while curr.next:
            curr = curr.next
            result.append(curr.data)
        return result 

    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None 
        i = 0
        curr = self.head
        while i < pos:
            curr = curr.next
            i += 1 
        return curr 

    def insertAfter(self, prev, newNode):
        newNode.next = prev.next
        if prev.next is None:
            self.tail = newNode
        prev.next = newNode
        self.nodeCount += 1
        return True 

    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False 
        if pos != 1 and pos == self.nodeCount + 1:
            prev = self.tail
        else:
            prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode) 

    def popAfter(self, prev):
        if prev == self.tail:
            return None
        curr = prev.next
        prev.next = curr.next
        if curr.next == None:
            self.tail = prev
        self.nodeCount -= 1
        return curr.data 

    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError
        return self.popAfter(self.getAt(pos-1))        

def solution(x):
    return 0 

Doubly Linked List

앞으로뿐만 아니라 뒤로도 진행 가능
- Node 구조 확장
- 리스트 처음과 끝에 dummy node 추가

class Node: 
    def __init__(self, item):
        self.data = item
        self.prev = None
        self.next = None

class DoublyLinkedList: 
    def __init__(self):
        self.nodeCount = 0
        self.head = Node(None)
        self.tail = Node(None)
        self.head.prev = None # 더미노드
        self.head.next = self.tail
        self.tail.prev = self.head
        self.tail.next = None # 더미노드


    def __repr__(self):
        if self.nodeCount == 0:
            return 'LinkedList: empty'

        s = ''
        curr = self.head
        while curr.next.next: # 더미노드까지
            curr = curr.next
            s += repr(curr.data)
            if curr.next.next is not None:
                s += ' -> '
        return s


    def getLength(self):
        return self.nodeCount


    def traverse(self):
        result = []
        curr = self.head
        while curr.next.next:
            curr = curr.next
            result.append(curr.data)
        return result


    def getAt(self, pos):
        if pos < 0 or pos > self.nodeCount:
            return None

        if pos > self.nodeCount // 2:
            i = 0
            curr = self.tail
            while i < self.nodeCount - pos + 1:
                curr = curr.prev
                i += 1
        else:
            i = 0
            curr = self.head
            while i < pos:
                curr = curr.next
                i += 1

        return curr


    def insertAfter(self, prev, newNode):
        next = prev.next
        newNode.prev = prev
        newNode.next = next
        prev.next = newNode
        next.prev = newNode
        self.nodeCount += 1
        return True


    def insertAt(self, pos, newNode):
        if pos < 1 or pos > self.nodeCount + 1:
            return False

        prev = self.getAt(pos - 1)
        return self.insertAfter(prev, newNode) 
    
    def popAfter(self, prev):
        curr = prev.next
        next = curr.next
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data

    def popBefore(self, next):
        curr = next.prev
        prev = curr.prev
        prev.next = next
        next.prev = prev
        self.nodeCount -= 1
        return curr.data


    def popAt(self, pos):
        if pos < 1 or pos > self.nodeCount:
            raise IndexError
        curr = self.getAt(pos)
        return self.popAfter(curr.prev)
    
     def concat(self, L):
        self.tail.prev.next = L.head.next
        L.head.next.prev = self.tail.prev
        self.tail = L.tail

        self.nodeCount += L.nodeCount

Stack

배열 기반

class ArrayStack:

	def __init__(self):
		self.data = []

	def size(self):
		return len(self.data)

	def isEmpty(self):
		return self.size() == 0

	def push(self, item):
		self.data.append(item)

	def pop(self):
		return self.data.pop()

	def peek(self):
		return self.data[-1]

연결리스트 기반

from doublylinkedlist import Node
from doublylinkedlist import DoublyLinkedList

class LinkedListStack:

	def __init__(self):
		self.data = DoublyLinkedList()

	def size(self):
		return self.data.getLength()

	def isEmpty(self):
		return self.size() == 0

	def push(self, item):
		node = Node(item)
		self.data.insertAt(self.size() + 1, node)

	def pop(self):
		return self.data.popAt(self.size())

	def peek(self):
		return self.data.getAt(self.size()).data

예제

수식의 괄호 검사

class ArrayStack:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]


def solution(expr):
    match = {
        ')': '(',
        '}': '{',
        ']': '['
    }
    S = ArrayStack()
    for c in expr:
        if c in '({[':
            S.push(c)
        elif c in match:
            if S.isEmpty():
                return False
            else:
                t = S.pop()
                if t != match[c]:
                    return False
    return S.isEmpty()

수식의 후위 표기법(Postfix Notation)

중위 표기법 (infix notation) - A + B
후위 표기법 (Postfix Notation) - AB+
- 괄호를 쓰지 않고도 연산의 우선순위를 수식에 표현
  - (A + B) * (C + D) 중위 -> A B + C D + * 후위
  - A + B * C 중위 -> A B C * + 후위
- 컴퓨터가 후위 표기법을 사용하면 수식을 만날 때마다 스택에 적용
연산자를 만나면 우선 스택에 넣는다.
연산자를 다시 만나면 스택에 있는 것과 비교해 우선순위가 높은 것을 팝해서 피연산자 뒤에 놓는다.
그러고 나서 만난 연산자를 스택에 넣는다.
수식의 끝에 도달하면 연산자를 팝해서 피연산자 뒤에 놓는다.
괄호의 처리
- 여는 괄호는 스택에 푸시
- 닫는 괄호를 만나면 여는 괄호가 나올 때까찌 pop
  - 괄호 안에 들어있는 연산을 우선 행하는 효과
- 연산자를 만났을 때, 여는 괄호 너머까지 pop하지 않도록
  - 여는 괄호의 우선순위는 가장 낮게 설정

중위표현 수식 –> 후위표현 수식

class ArrayStack:

    def __init__(self):
        self.data = []

    def size(self):
        return len(self.data)

    def isEmpty(self):
        return self.size() == 0

    def push(self, item):
        self.data.append(item)

    def pop(self):
        return self.data.pop()

    def peek(self):
        return self.data[-1]

prec = {
    '*': 3, '/': 3,
    '+': 2, '-': 2,
    '(': 1
}

def solution(S):
    opStack = ArrayStack()
    answer = ''
    for i in S:
        if i not in prec and i != ')':
            answer += i
        elif i == '(':
            opStack.push(i)
        elif i == ')':
            while opStack.peek() != '(':
                answer += opStack.pop()
            opStack.pop()
        elif opStack.isEmpty():
            oStack.push(i)
        else:
            while not opStack.isEmpty() and prec[opStack.peek()] >= prec[i]:
                answer += opStack.pop()
            opStack.push(i)
    while not opStack.isEmpty():
        answer += opStack.pop()
    return answer

큐

넣을 때는 한쪽 끝에서 밀어 넣어야 하고
- 인큐(enqueue) 연산 - 배열 O(1), 이중연결리스트
꺼낼 때는 반대 쪽에서 꺼내야 하는 제약이 있음
- 디큐(dequeue) 연산 - 배열 O(n), 이중연결리스트

from pythonds.basic.queue import Queue

Q = Queue()
dir(Q)

큐의 활용

자료를 생성하는 작업과 그 자료를 이용하는 작업이 비동기적으로 일어나는 경우
자료를 생성하는 작업이 여러 곳에서 일어나는 경우
자료를 생성하는 작업과 그 자료를 이용하는 작업이 양쪽 다 여러 곳에서 일어나는 경우
자료를 처리하여 새로운 자료를 생성하고, 나중에 그 자료를 또 처리해야 하는 작업의 경우

환형 큐

정해진 개수의 저장 공간을 빙 돌려가며 이용
rear - 데이터 넣는 포인트, front - 데이터 빼는 포인트
큐 가득 차면?
- 더이상 원소를 넣을 수 없음(큐 길이를 기억하고 있어야)
디큐한 자리까지 데이터가 가득 차면?
- 무효가 된 자리를 덮어쓰면 된다.
- 한계치를 넘어가면 다시 0으로 돌아간다.

초기에 front 와 rear 를 공히 -1 로 초기화한 후에, (1) enqueue 연산의 경우 rear 를 전진시키고 (+1) 그 위치에 원소를 삽입하고 (2) dequeue 연산의 경우 front 를 전진시키고 (+1) 그 위치의 원소를 리턴한다. 이렇게 함으로써 리스트 data 를 인덱스 0 부터 이용하게 되며, front 는 큐에서 가장 앞에 들어 있는 원소 (현재 큐에 들어 있는 원소들 중 가장 먼저 삽입된 원소) 를 가리키고 있지 않고 그보다 하나 작은 인덱스를 가지고 있게 된다.
front 와 rear 의 전진에서는 환형 구조를 위하여 1 을 더하는 것 외에도 큐의 크기로 나눈 나머지를 취하는 연산이 수반되어야 함

class CircularQueue:

    def __init__(self, n):
        self.maxCount = n
        self.data = [None] * n
        self.count = 0
        self.front = -1
        self.rear = -1


    def size(self):
        return self.count

    def isEmpty(self):
        return self.count == 0

    def isFull(self):
        return self.count == self.maxCount

    def enqueue(self, x):
        if self.isFull():
            raise IndexError('Queue full')
        self.rear = (self.rear+1)% self.maxCount
        self.data[self.rear] = x
        self.count += 1

    def dequeue(self):
        if self.size() == 0:
            raise IndexError('Queue empty')
        self.front = (self.front+1) % self.maxCount
        x = self.data[self.front]
        self.count -= 1
        return x

    def peek(self):
        if self.isEmpty():
            raise IndexError('Queue empty')
        return self.data[(self.front+1) % self.maxCount]


def solution(x):
    return 0

우선순위 큐

원소들의 우선순위에 따라 큐에서 빠져나오는 방식
- 예: 운영체제의 CPU 스케줄러

2가지 큐의 구현

Enqueue 할 때 우선순위 순서를 유지하도록
Dequeue 할 때 우선순위 높은 것을 선택
- Enqueue가 더 유리하다
- 모든 원소를 쳐다볼 필요 없다. 우선순위가 있기 때문에
선형 배열 이용
연결 리스트 이용
- 시간 유리. 요소 삽입 시 배열에 비해 수월. 배열은 다른 요소들까지 각각 자리를 밀어야 하지만 연결리스트는 끊고 들어가면 되므로
- 메모리 불리. 배열보다 많이 차지

더블연결리스트 우선수위 큐

작은 수가 우선순위가 높다는 가정
while 1 조건 - 끝을 만나지 않았을 조건, 2 조건 우선순위를 비교하는 조건
getAt() 메서드를 이용하지 않음
- 왜? 계속 세면서 나가야 하므로
예: [1,2,4,6,8,10] 인데 5를 넣는다면?
- 이 순환문이 하는 일은 큐의 앞쪽부터 시작해서 처음으로 newNode.data보다 같거나 큰 데이터가 ㄱ나타나는 노드를 찾ㅇㅏ 그 직전의 것을 curr에 담는 것
- 처음으로 newNode.data < curr.next.data를 만족하지 못하는 경우는 curr.next.data가 6인 경우
- curr는 원소 4를 가지는 노드를 가리킨다. 이 노드의 다음에 원소 5를 가지는 노드를 삽입

class PriorityQueue:

    def __init__(self):
        self.queue = DoublyLinkedList()


    def size(self):
        return self.queue.getLength()

    def isEmpty(self):
        return self.size() == 0

    def enqueue(self, x):
        newNode = Node(x)
        curr = self.queue.head ## 문제
        while curr.next.data != None and newNode.data < curr.next.data: ## 문제
            curr = curr.next
        self.queue.insertAfter(curr, newNode) ## 문제
    
    def dequeue(self):
        return self.queue.popAt(self.queue.getLength())

    def peek(self):
        return self.queue.getAt(self.queue.getLength()).data

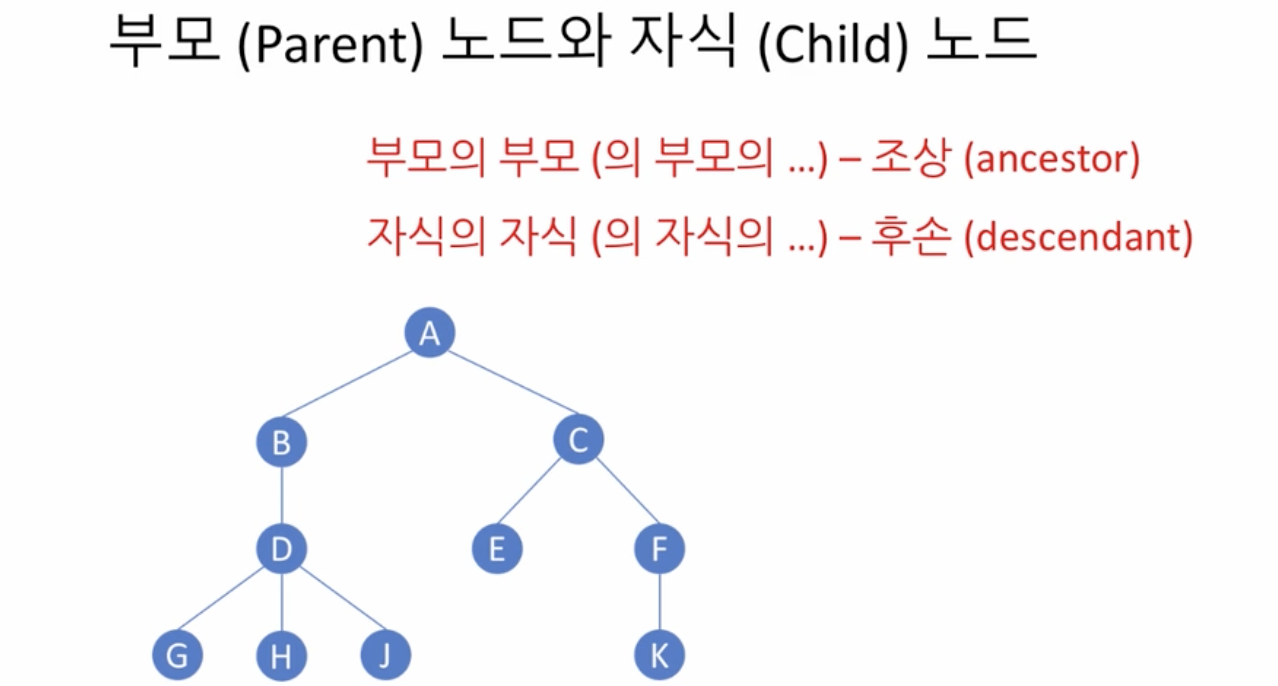
트리

설명

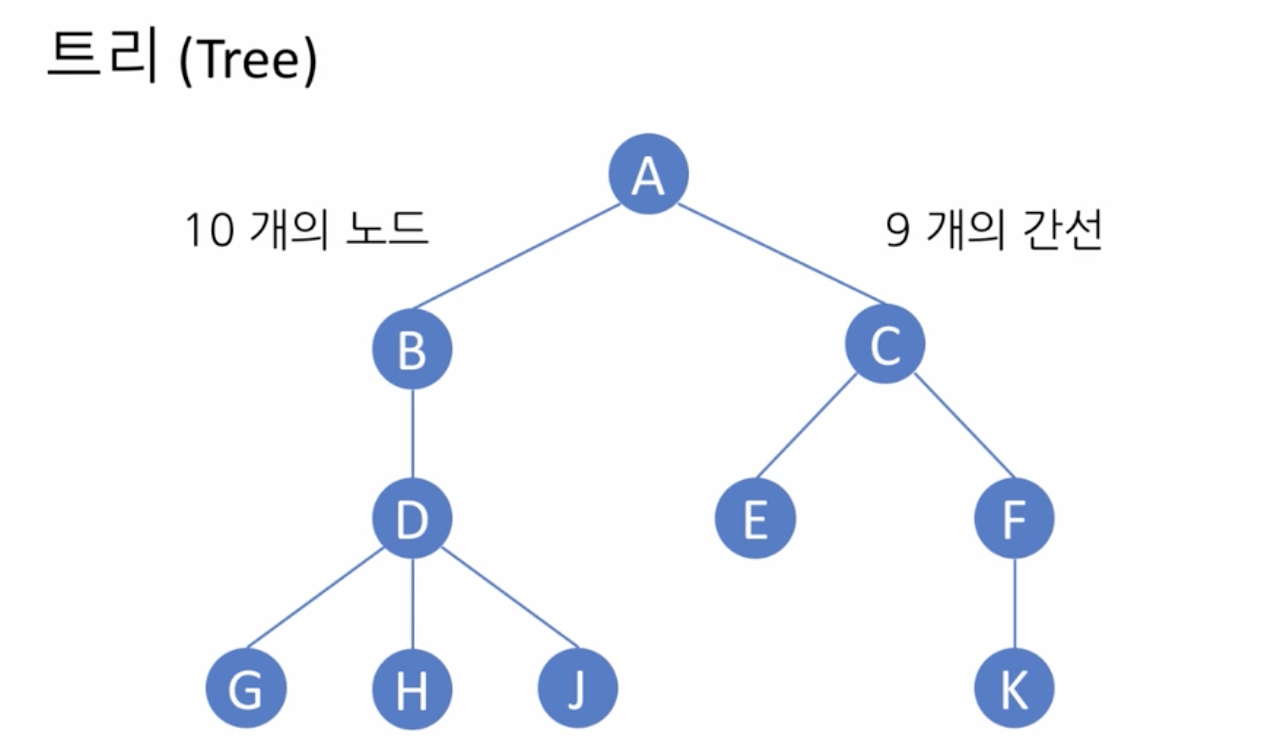
정점(node)과 간선(edge)을 이용하여 데이터의 배치 형태를 추상화한 자료구조
이진 트리
- 모든 노드의 차수가 2 이하인 트리
- 포화 이진 트리
  - 모든 레벨에서 노드들이 모두 채워져 있는 이진 트리
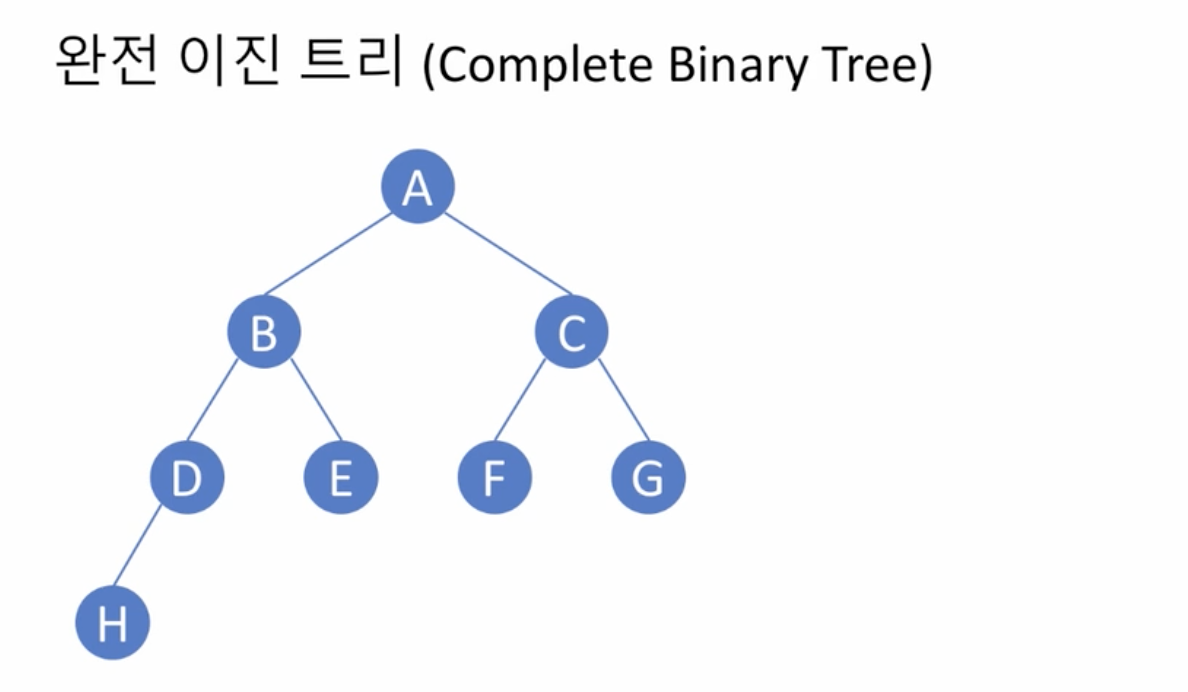
- 완전 이진 트리
  - 높이 k인 완전 이진 트리
  - 레벨 k - 2까지는 모든 노드가 2개의 자식을 가진 포화 이진 트리
  - 레벨 k - 1에서는 왼쪽부터 노드가 순차적으로 채워져 있는 이진 트리

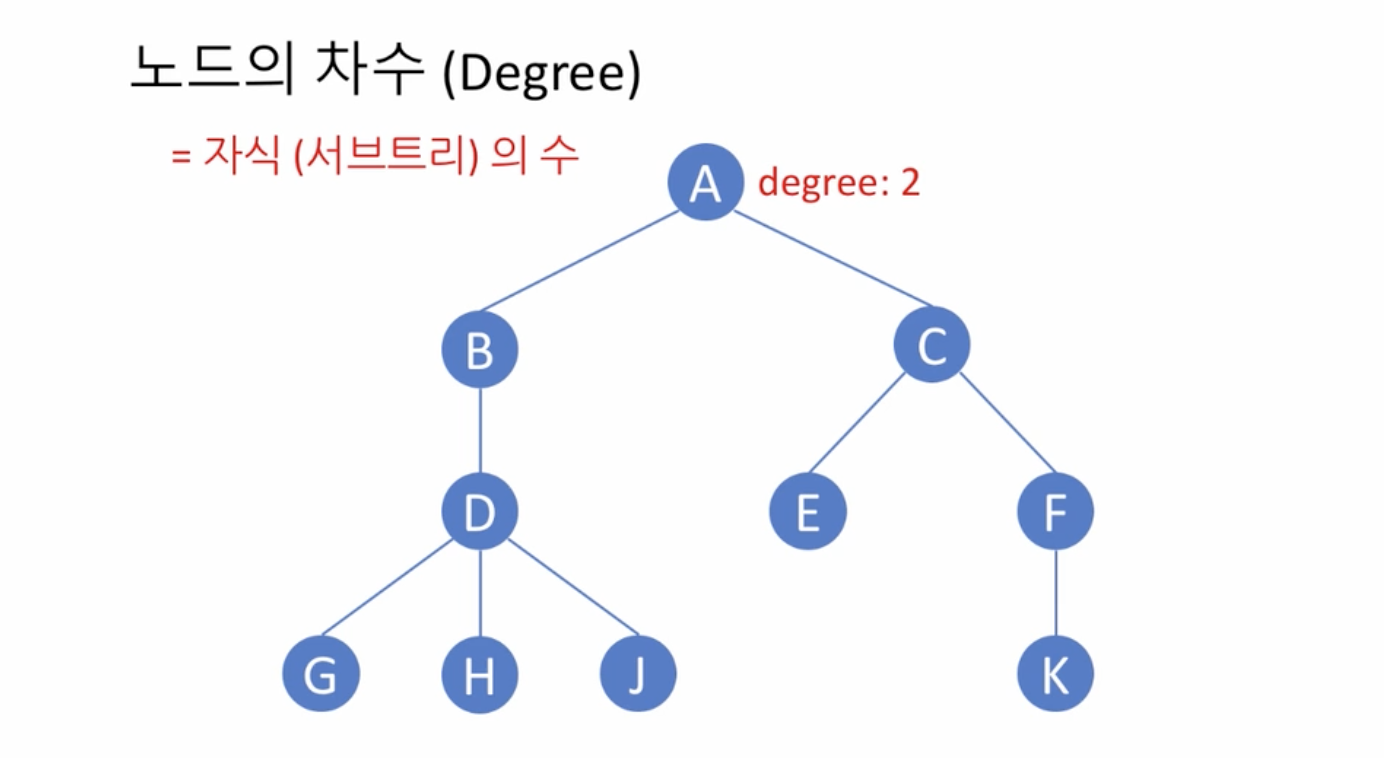
이진 트리의 구현

`depth()`, `size()`

class Node:
    def __init__(self, item):
        self.data = item
        self.left = None
        self.right = None

    def size(self):
        l = self.left.size() if self.left else 0
        r = self.right.size() if self.right else 0
        return l + r + 1

    def depth(self):
        l = self.left.depth() if self.left else 0
        r = self.right.depth() if self.right else 0
        return max([l, r]) + 1

class BinaryTree:
    def __init__(self, r):
        self.root = r

    def size(self):
        if self.root:
            return self.root.size()
        else:
            return 0

    def depth(self):
        if self.root:
            return self.root.depth()
        else:
            return 0

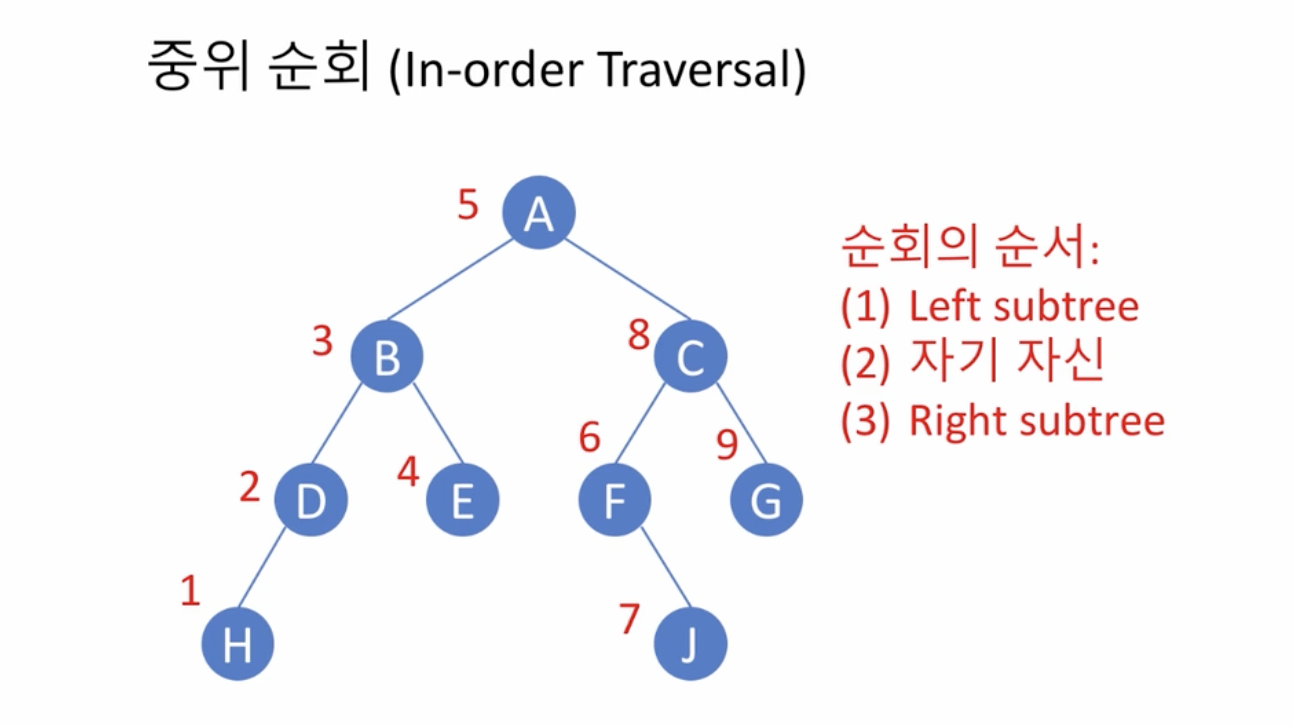
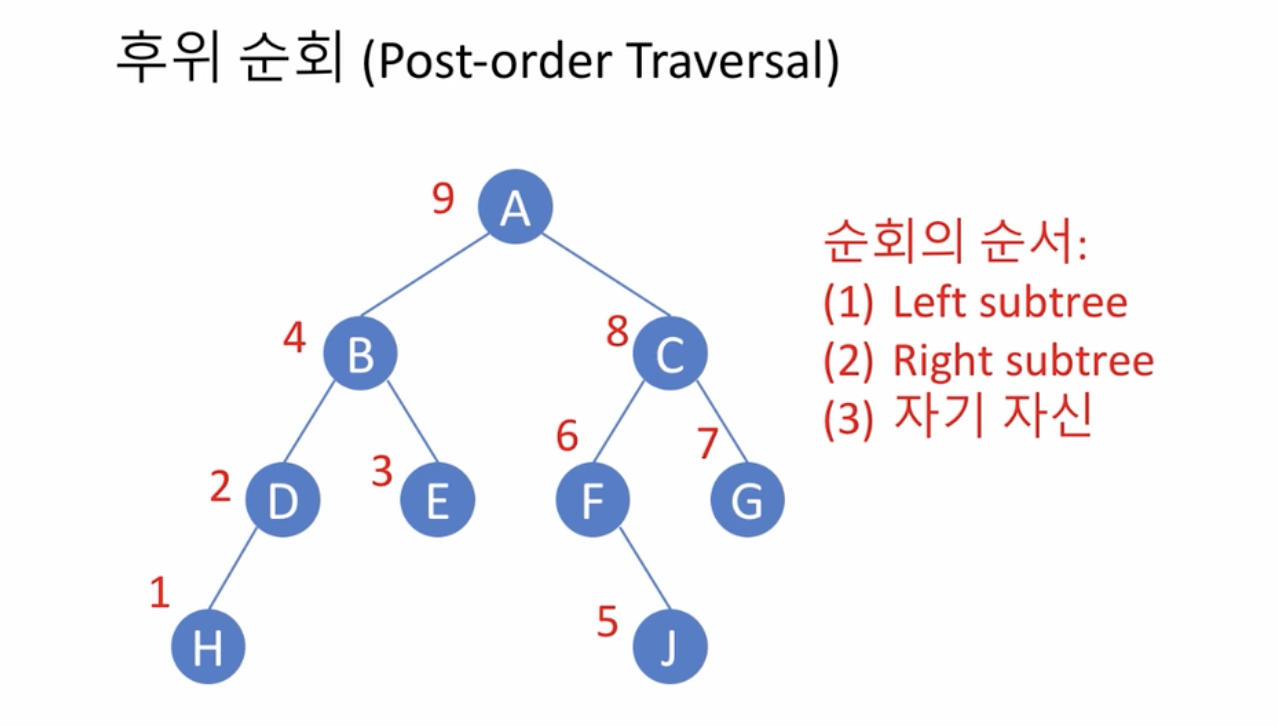
이진 트리의 순회(Traversal)

깊이 우선 순회(depth first traversal)
- 중위 순회(in-order traversal)
- 전위 순회(pre-order traversal)
- 후위 순회(post-order traversal)
- 자기 자신을 중간에 방문 - 중위, 자기 자신을 먼저 방문 - 전위
넓이 우선 순회(breadth first traversal)

깊이 우선 순회

중위 우선 순회

스크린샷 2020-06-02 오전 9 28 31

class Node

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder() # 1 leftsubtree
        traversal.append(self.data) # 2 자기 자신
        if self.right:
            traversal += self.right.inorder() # rightsubtree
        return traversal

class binaryTree:
    def inorder(self):
        if self.root:
            return self.toor.inonder()
        else:
            return []

스크린샷 2020-06-02 오전 9 37 00

스크린샷 2020-06-02 오전 9 39 04

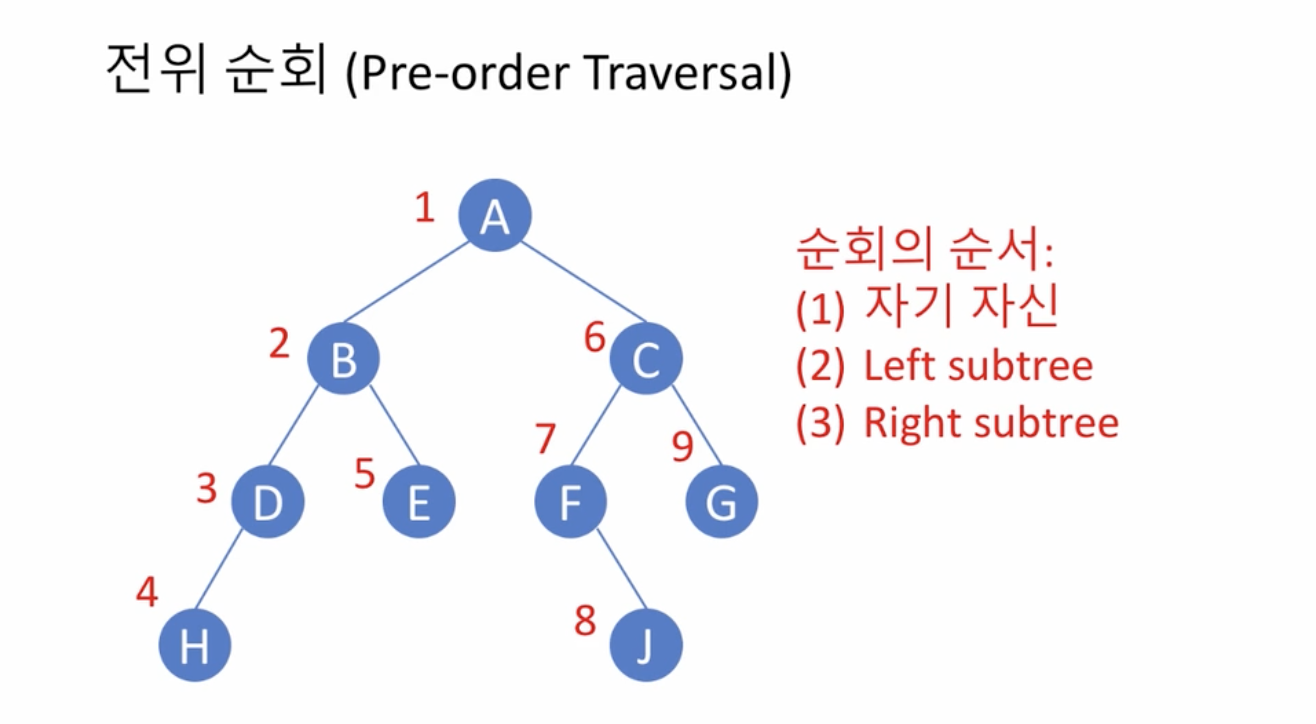
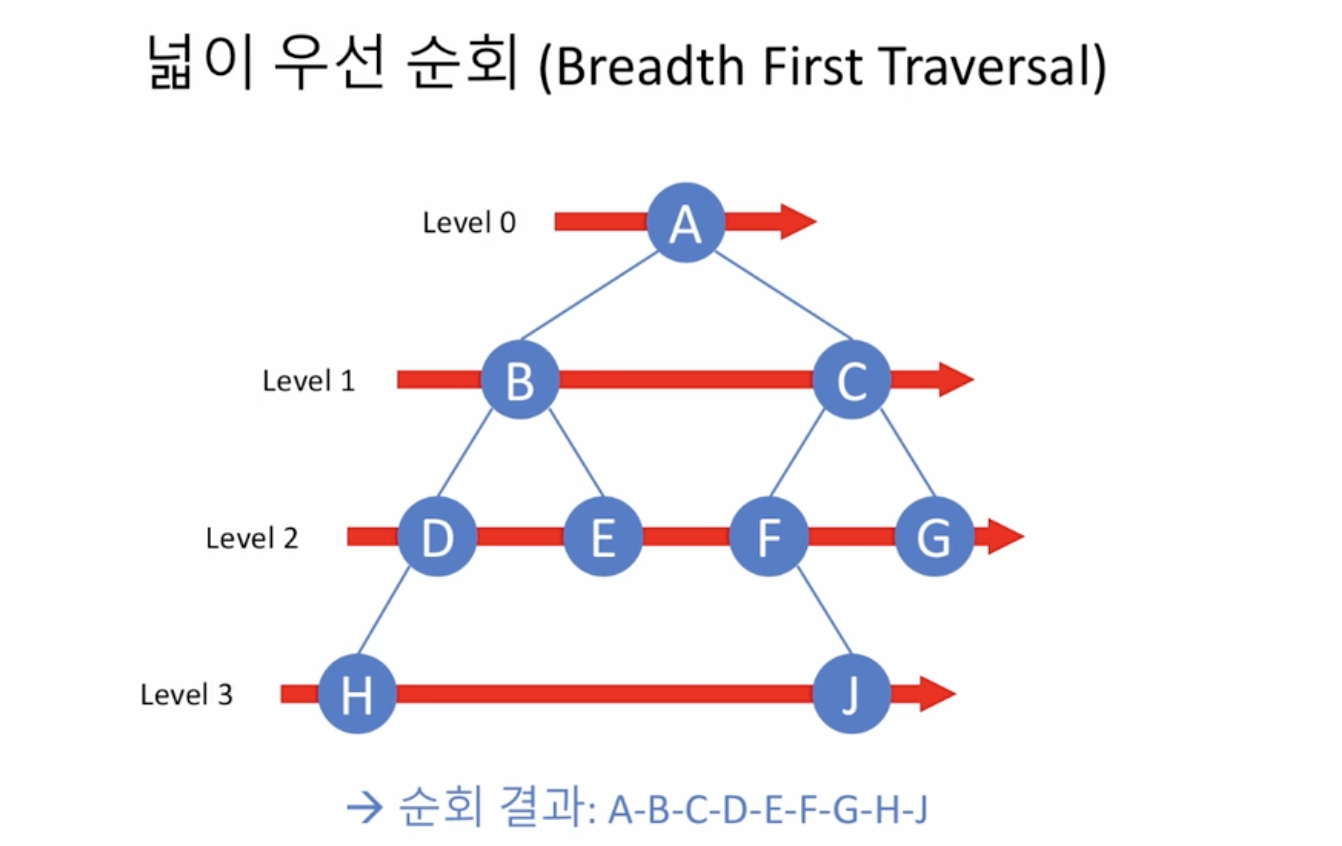
넓이 우선 순회(breadth first traversal)

원칙
- 수준(level)이 낮은 노드를 우선으로 방문
- 같은 수준의 노드들 사이에는
  - 부모 노드의 방문 순서에 따라 방문
  - 왼쪽 자식 노드를 오른쪽 자식보다 먼저 방문
재귀적 방법이 적합한가? No
- 한 노드를 방문했을 때
  - 나중에 방문할 노드들을 순서대로 기록해 두어야
  - 큐를 이용하면 어떨까?

스크린샷 2020-06-03 오전 9 36 12

스크린샷 2020-06-03 오전 9 41 39

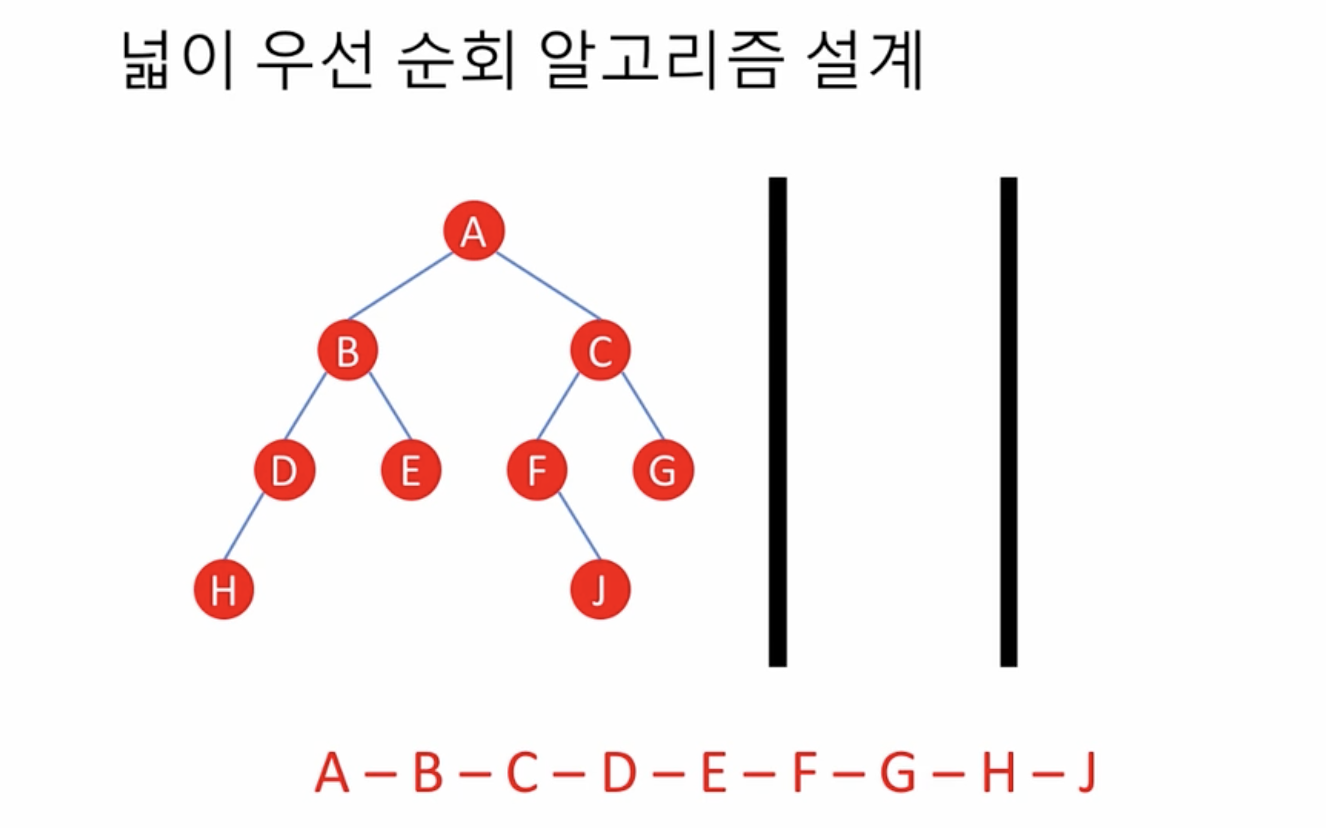
알고리즘 구현

(초기화) traversal <- 빈 리스트, q <- 빈 큐
빈 트리가 아니면, root node를 q에 추가(enqueue)
q가 비어 있지 않은 동안
- node <- q에서 원소를 추출(dequeue)
- node를 방문
- node의 왼쪽, 오른쪽 자식(있으면)들을 q에 추가
q가 빈 큐가 되면 모든 노드 방문 완료

class BinaryTree:
    def __init__(self, r):
        self.root = r

    def bft(self):
        q = ArrayQueue()
        traversal = []
        if self.root:
            q.enqueue(self.root)
        while not q.isEmpty():
            node = q.dequeue()
            traversal.append(node.data)
            if node.left:
                q.enqueue(node.left)
            if node.right:
                q.enqueue(node.right)
        return traversal

이진 탐색 트리

모든 노드에 대해서,
- 왼쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 작고
- 오른쪽 서브트리에 있는 데이터는 모두 현재 노드의 값보다 크다
정렬된 배열을 이용한 이진탐색과 비교
- 장점: 데이터 원소의 추가, 삭제가 용이
- 단점: 공간 소요가 큼
이진 탐색 트리의 추상적 자료구조
- 각 노드를 키, 밸류 상으

class BinSearchTree:
    def lookup(self, key):
        if self.root:
            return self.root.lookup(key)
        else:
            return None, None # 찾은 노드, 부모 노드

class Node:
    def lookup(self, key, parent=None):
        if key < self.key:
            if self.left:
                return self.left.lookup(key, self)
            else:
                reutnr None, None

이진 탐색 트리 원소 삽입 연산 구현

class Node:
    def __init__(self, key, data):
        self.key = key
        self.data = data
        self.left = None
        self.right = None

    def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
            else:
                self.right = Node(key, data)
        else:
            raise KeyError('Key %s already.' % key)

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self)
        if self.right:
            traversal += self.right.inorder()
        return traversal

class BinSearchTree:
    def __init__(self):
        self.root = None

    def insert(self, key, data):
        if self.root:
            self.root.insert(key, data)
        else:
            self.root = Node(key, data)

    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

이진 탐색 트리에서 원소 삭제

키를 이용해서 노드를 찾는다
- 해당 키의 노드가 없으면, 삭제할 것도 없음
- 찾은 노드의 부도 노드도 알고 있어야 함
찾은 노드를 제거하고도 이진 탐색 트리 성질을 만족하도록 트리의 구조를 정리
- 삭제되는 노드가
  - 말단(leaf) 노드인 경우
    - 그냥 그 노드를 없애면 됨
    - 부모 노드의 링크를 조정(좌? 우?)
    - 삭제되는 노드가 root node인 경우?
      - 트리 전체를 삭제
  - 자식을 하나 가지고 있는 경우
    - 삭제되는 노드 자리에 그 자식을 대신 배치
      - 자식이 좌? 우?
      - 부모 노드의 링크를 조정(좌? 우?)
      - 삭제되는 노드가 root node인 경우?
        
        대신 들어오는 자식이 새로 root가 됨
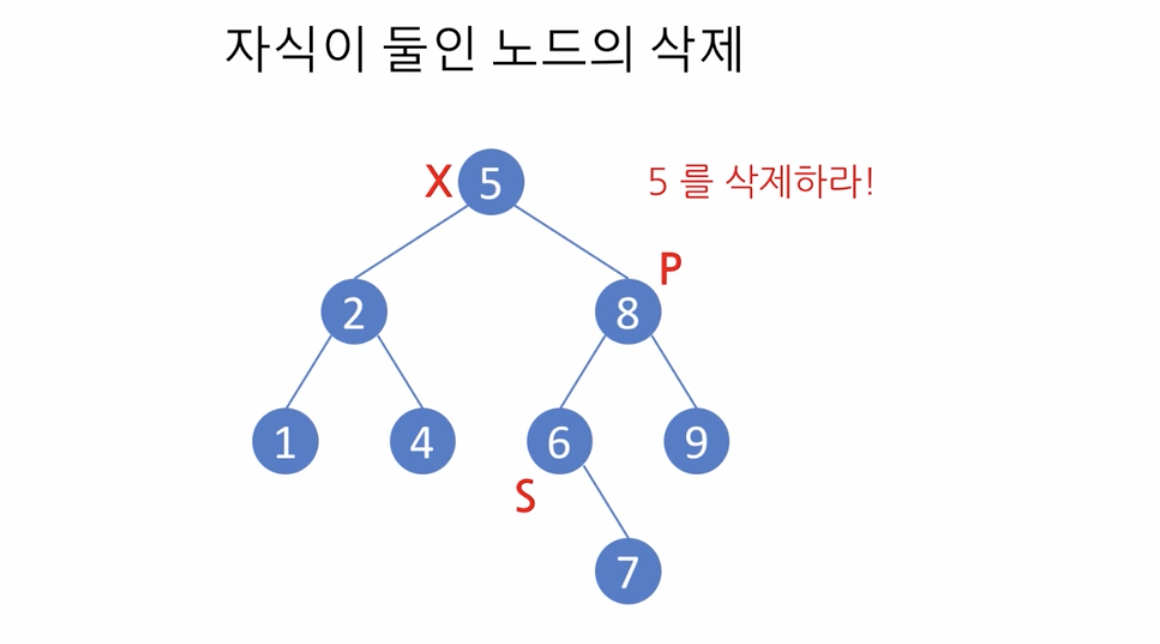
  - 자식을 둘 가지고 있는 경우
    - 삭제되는 노드보다 바로 다음 (큰) 키(작은도 가능)를 가지는 노드를 찾아
    - 그 노드를 삭제되는 노드 자리에 대신 배치하고 이 노드를 대신 삭제
    - Successor
      - 삭제될 노드보다 1 큰 노드
      - 삭제될 노드의 오른쪽에서 가장 작은 노드

스크린샷 2020-06-05 오전 10 15 30

이진 탐색 트리가 별로 효율적이지 못한 경우
- 선형 탐색과 동일한 복잡도

스크린샷 2020-06-05 오전 10 22 16

보다 나은 성능을 보이는 이진 탐색 트리들
- 높이의 균형을 유지함으로써 O(logn)의 탐색 복잡도 보장
- 삽입, 삭제 연산이 보다 복잡
  - AVL tree
  - Red-black tree

class Node:
    def __init__(self, key, data):
        self.key = key
        self.data = data
        self.left = None
        self.right = None

    def insert(self, key, data):
        if key < self.key:
            if self.left:
                self.left.insert(key, data)
            else:
                self.left = Node(key, data)
        elif key > self.key:
            if self.right:
                self.right.insert(key, data)
            else:
                self.right = Node(key, data)
        else:
            raise KeyError('Key %s already exists.' % key)

    def lookup(self, key, parent=None):
        if key < self.key:
            if self.left:
                return self.left.lookup(key, self)
            else:
                return None, None
        elif key > self.key:
            if self.right:
                return self.right.lookup(key, self)
            else:
                return None, None
        else:
            return self, parent

    def inorder(self):
        traversal = []
        if self.left:
            traversal += self.left.inorder()
        traversal.append(self)
        if self.right:
            traversal += self.right.inorder()
        return traversal

    def countChildren(self):
        count = 0
        if self.left:
            count += 1
        if self.right:
            count += 1
        return count


class BinSearchTree:
    def __init__(self):
        self.root = None

    def insert(self, key, data):
        if self.root:
            self.root.insert(key, data)
        else:
            self.root = Node(key, data)

    def lookup(self, key):
        if self.root:
            return self.root.lookup(key)
        else:
            return None, None

    def remove(self, key):
        node, parent = self.lookup(key)
        if node:
            nChildren = node.countChildren()
            # [Case 1]: The simplest case of no children
            if nChildren == 0:
                # 만약 parent 가 있으면
                # node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여 parent.left 또는 parent.right 를 None 으로 하여
                # leaf node 였던 자식을 트리에서 끊어내어 없앱니다.
                if parent:
                    if parent.left == node:
                        parent.left = None
                    else:
                        parent.right = None

                # 만약 parent 가 없으면 (node 는 root 인 경우) self.root 를 None 으로 하여 빈 트리로 만듭니다.
                else:
                    self.root = None

            # [Case 2]: When the node has only one child
            elif nChildren == 1:
                # 하나 있는 자식이 왼쪽인지 오른쪽인지를 판단하여 그 자식을 어떤 변수가 가리키도록 합니다.
                # 만약 parent 가 있으면 node 가 왼쪽 자식인지 오른쪽 자식인지 판단하여
                # 위에서 가리킨 자식을 대신 node 의 자리에 넣습니다.
                if parent:
                    if node.left:
                        if parent.left == node:
                            parent.left = node.left
                        else:
                            parent.right = node.left
                    else:
                        if parent.right == node:
                            parent.right = node.right
                        else:
                            parent.right = node.right

                # 만약 parent 가 없으면 (node 는 root 인 경우) self.root 에 위에서 가리킨 자식을 대신 넣습니다.
                else:
                    if node.left:
                        self.root = node.left
                    else:
                        self.root = node.right

            # [Case 3]: When the node has both left and right children
            else:
                parent = node
                successor = node.right
                # parent가 node를 가리키도록 하고,
                # successor 는 node 의 오른쪽 자식 서브트리의 root노드를 가리키도록 합니다.
                # successor 로부터 왼쪽 자식의 링크를 반복하여 따라감으로써
                # 순환문이 종료할 때 successor는 node의 오른쪽 자식 서브트리의 최소값을,
                # 그리고 parent 는 그 노드의 부모 노드를 가리키도록 찾아냅니다.

                while successor.left:
                    parent = successor
                    successor = successor.left
                # 삭제하려는 노드인 node 에 방금 찾은 successor 의 key 와 data 를 대입합니다.
                node.key = successor.key
                node.data = successor.data
                # 이제, successor 가 parent 의 왼쪽 자식인지 오른쪽 자식인지를 판단하여
                # 그에 따라 parent.left 또는 parent.right 를 successor 가 가지고 있던 (없을 수도 있지만) 자식을 가리키도록 합니다.
                if parent.left == successor:
                    if successor.left:
                        parent.left = successor.left
                    elif successor.right:
                        parent.left = successor.right
                    else: parent.left = None
                else:
                    if successor.left:
                        parent.right = successor.left
                    elif successor.right:
                        parent.right = successor.right
                    else:
                        parent.right = None
            return True
        else:
            return False

    def inorder(self):
        if self.root:
            return self.root.inorder()
        else:
            return []

힙(heap)

이진 트리의 한 종류(이진 힙 - binary heap)
- 루트 노드가 언제나 최댓값 또는 최솟값을 가짐
  - 최대 힙(max head), 최소 힙(min heap)
- 완전 이진 트리여야 함

Maxheap

최대 힙의 예
- 자식보다 부모가 큰 값을 가진다
- 재귀적으로도 정의됨
  - 어느 노드를 루트로 하는 서브트리도 모두 최대 힙
- 그러나 자식들의 대소관계는 정해지지 않음 - 느슨한 관계

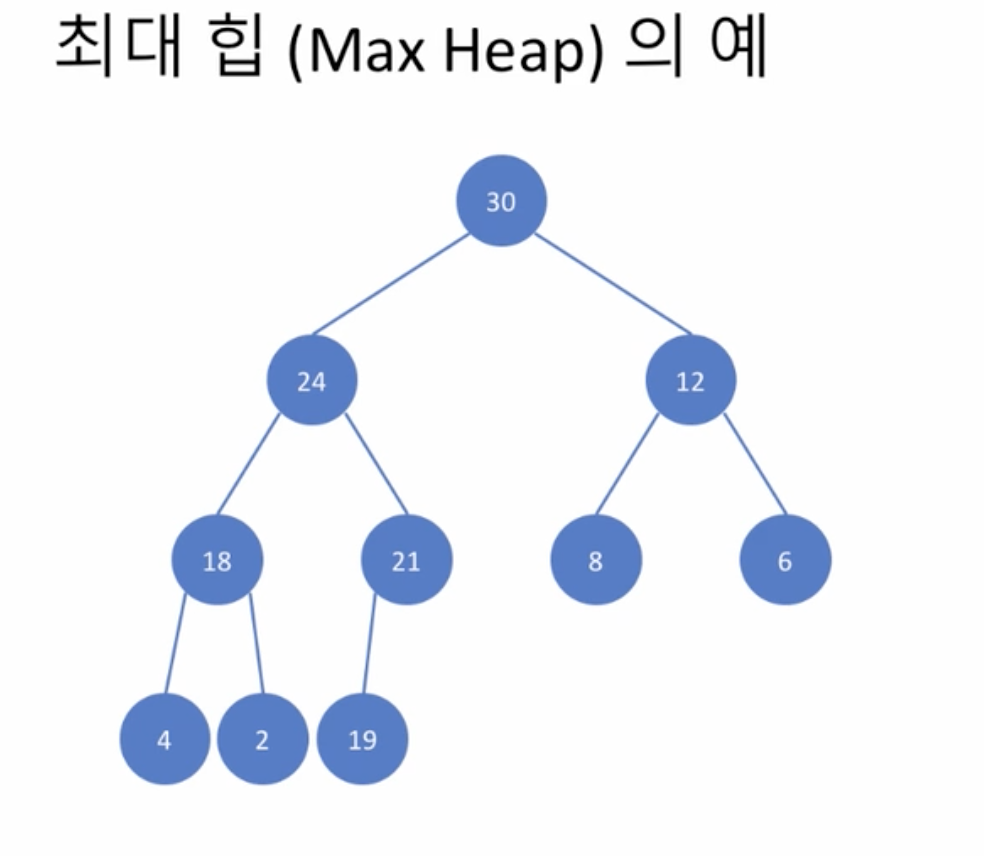
이진 탐색 트리와의 비교
- 원소들은 완전히 크기 순으로 정렬되어 있는가?
- 특정 키 값을 가지는 원소를 빠르게 검색할 수 있는가?
- 부가의 제약 조건은 어떤 것인가?
최대 힙 연산 정의
- remove() - 최대 원소(root node)를 반환
  - 동시에 이 노드를 삭제
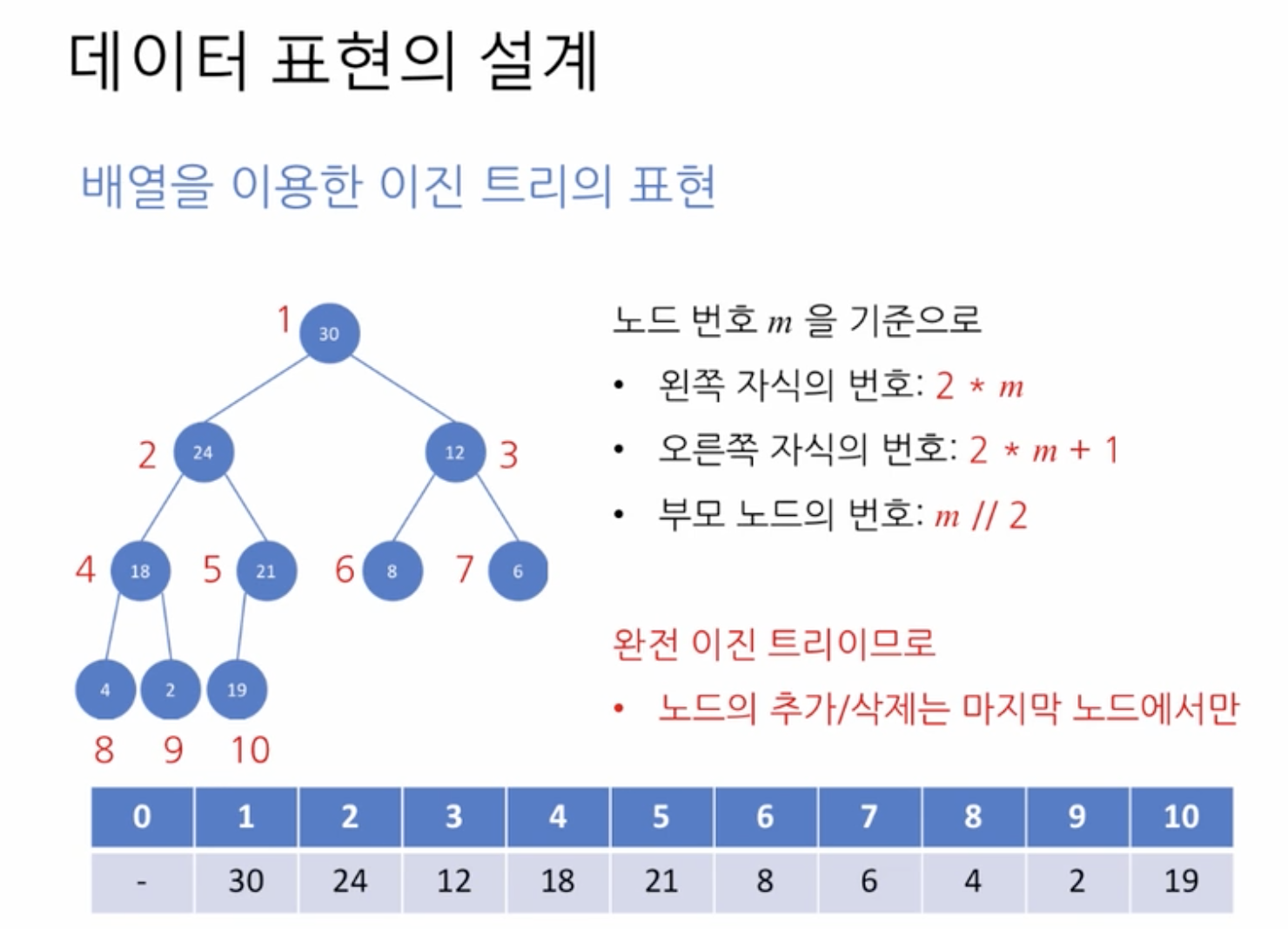
데이터 표현의 설계
- 완전 이진 트리이므로 배열로 표현하기 적당
- 0이 아닌 1부터 인덱스 시작

class MaxHeap:
    def __init__(self):
        self.data = [None] # 0이 아닌 1부터 시작하므로

최대 힙에 원소 삽입

최대 힙에 원소 삽입
- 트리의 마지막 자리에 새로운 원소를 임시로 저장
- 부모 노드와 키 값을 비교하여 위로, 위로 이동

class MaxHeap:
    def __init__(self):
        self.data = [None]

    def insert(self, item):
        self.data.append(item)
        i = len(self.data) - 1 
        while i > 1:
            if self.data[i] > self.data[(i // 2)]:
                self.data[i], self.data[(i // 2)] = self.data[(i // 2)], self.data[i]
                i = i // 2
            else:
                break

최대 힙에서 원소의 삭제

루트 노드의 제거 - 이것이 원소들 중 최댓값 [1]
트리 마지막 자리 노드를 임시로 루트 노드의 자리에 배치 [2]
자식 노드들과의 값 비교와 아래로, 아래로 이동 [3]
- 자식이 둘 있다면 더 큰 값부터 아래로, 아래
  - 더 큰 값이 위로 올라와야 하므로

class MaxHeap:
    def remove(self):
        if len(self.data) > 1: # 0은 안 쓰므로
            self.data[1], self.data[-1] = self.data[-1], self.data[1] # 2
            data = self.data.pop(-1) # 1
            self.maxHeapify(1) # 3
        else:
            data = None
        return data

 def maxHeapify(self, i):
        # 왼쪽 자식 (left child) 의 인덱스를 계산합니다.
        left =i*2

        # 오른쪽 자식 (right child) 의 인덱스를 계산합니다.
        right =2*i+1

        smallest = i
        # 왼쪽 자식이 존재하는지, 그리고 왼쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if left <len(self.data) and self.data[left] > self.data[smallest] :
            # 조건이 만족하는 경우, smallest 는 왼쪽 자식의 인덱스를 가집니다.
            smallest = left

        # 오른쪽 자식이 존재하는지, 그리고 오른쪽 자식의 (키) 값이 (무엇보다?) 더 큰지를 판단합니다.
        if right < len(self.data) and self.data[right] > self.data[smallest]:
            # 조건이 만족하는 경우, smallest 는 오른쪽 자식의 인덱스를 가집니다.
            smallest = right

        if smallest != i:
            # 현재 노드 (인덱스 i) 와 최댓값 노드 (왼쪽 아니면 오른쪽 자식) 를 교체합니다.
            self.data[smallest], self.data[i] = self.data[i], self.data[smallest]

            # 재귀적 호출을 이용하여 최대 힙의 성질을 만족할 때까지 트리를 정리합니다.
            self.maxHeapify(smallest)

최대, 최소힙의 응용

힙 정렬

def heapsort(unsorted):
    H = MaxHeap()
    for item in unsorted:
        H.insert(item)
    sorted = []
    d = H.remove()
    while d:
        sorted.append(d)
        d = H.remove()
    return sorted

Link

어서와, 자료구조와 알고리즘은 처음이지?