algorithm
- 알고리즘 성능 표기법
- 기본정렬-버블정렬
- 기본정렬-삽입정렬
- 기본정렬-선택정렬 (최솟값)
- 재귀
- 동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer)
- 퀵 정렬 (quick sort)
- 병합 정렬(merge sort)
- 그래프 이해
- 그래프 알고리즘
- Link
알고리즘 성능 표기법
Big O (빅-오) 표기법: O(N)
- 알고리즘 최악의 실행 시간을 표기
- 아무리 최악의 상황이라도, 이정도의 성능은 보장한다는 의미이기 때문
- O(입력)
- 입력 n 에 따라 결정되는 시간 복잡도 함수
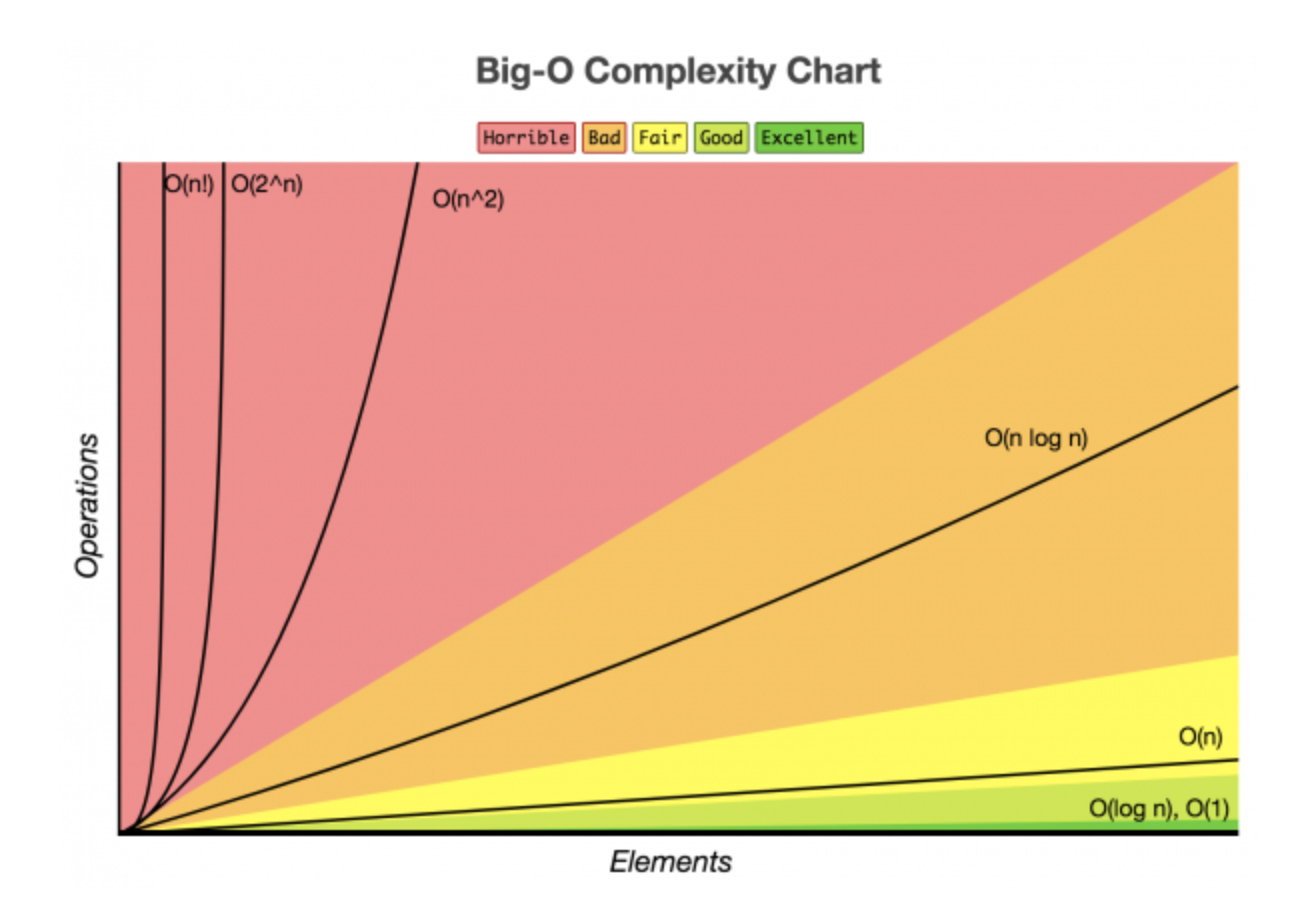
- O(1), O( 𝑙𝑜𝑔𝑛 ), O(n), O(n 𝑙𝑜𝑔𝑛 ), O( 𝑛2 ), O( 2𝑛 ), O(n!)등으로 표기함
- 입력 n 의 크기에 따라 기하급수적으로 시간 복잡도가 늘어날 수 있음
- O(1) < O( 𝑙𝑜𝑔𝑛 ) < O(n) < O(n 𝑙𝑜𝑔𝑛 ) < O( 𝑛2 ) < O( 2𝑛 ) < O(n!)
- 참고: log n 의 베이스는 2 - 𝑙𝑜𝑔2𝑛
- O(1) < O( 𝑙𝑜𝑔𝑛 ) < O(n) < O(n 𝑙𝑜𝑔𝑛 ) < O( 𝑛2 ) < O( 2𝑛 ) < O(n!)
- logn nlog 참고
# n에 따라, 𝑛2 번, 𝑛2 + 1000 번, 100 𝑛2 - 100, 또는 300 𝑛2 + 1번등 실행한다: O( 𝑛2 )
variable = 1
for i in range(300):
for num in range(n):
for index in range(n):
print(index)
- 빅 오 입력값 표기 방법
- 예: 만약 시간 복잡도 함수가 2 𝑛2 + 3n 이라면
- 가장 높은 차수는 2 𝑛2
- 상수는 실제 큰 영향이 없음
- 결국 빅 오 표기법으로는 O( 𝑛2 ) (서울부터 부산까지 가는 자동차의 예를 상기)
- 예: 만약 시간 복잡도 함수가 2 𝑛2 + 3n 이라면
- 반복문이 없으면 O(1), 있으면 O(n). 이중반복 O(𝑛2)
Ω (오메가) 표기법: Ω(N)
오메가 표기법은 알고리즘 최상의 실행 시간을 표기
Θ (세타) 표기법: Θ(N)
세타 표기법은 알고리즘 평균 실행 시간을 표기
- 시간 복잡도 계산은 반복문이 핵심 요소임을 인지하고, 계산 표기는 최상, 평균, 최악 중, 최악의 시간인 Big-O 표기법을 중심으로 익히면 됨
기본정렬-버블정렬
알고리즘 연습방법
- 연습장과 펜을 준비
- 간단한 경우부터 복잡한 순서대로 생각
- 가능한 알고리즘이 보인다면 구현 세부 항목을 나눠서 적는다
- 데이터구조, 변수 정리
- 각 문장을 코드로 적는다
버블정렬이란?
간단한 경우부터 복잡한 경우 순서대로 생각
-
데이터 2개일 떄, 3개일 때, 4개일 떄…
- 데이터가 네 개 일때 (데이터 개수에 따라 복잡도가 떨어지는 것은 아니므로, 네 개로 바로 로직을 이해해보자.)
- 예: data_list = [1, 9, 3, 2]
- 1차 로직 적용
- 1 와 9 비교, 자리바꿈없음 [1, 9, 3, 2]
- 9 와 3 비교, 자리바꿈 [1, 3, 9, 2]
- 9 와 2 비교, 자리바꿈 [1, 3, 2, 9]
- 2차 로직 적용
- 1 와 3 비교, 자리바꿈없음 [1, 3, 2, 9]
- 3 과 2 비교, 자리바꿈 [1, 2, 3, 9]
- 3 와 9 비교, 자리바꿈없음 [1, 2, 3, 9]
- 3차 로직 적용
- 1 과 2 비교, 자리바꿈없음 [1, 2, 3, 9]
- 2 과 3 비교, 자리바꿈없음 [1, 2, 3, 9]
- 3 과 9 비교, 자리바꿈없음 [1, 2, 3, 9]
특이점 찾아보기
- n개의 리스트가 있는 경우 최대 n-1번의 로직을 적용한다.
- 로직을 1번 적용할 때마다 가장 큰 숫자가 뒤에서부터 1개씩 결정된다.
- 로직이 경우에 따라 일찍 끝날 수도 있다. 따라서 로직을 적용할 때 한 번도 데이터가 교환된 적이 없다면 이미 정렬된 상태이므로 더 이상 로직을 반복 적용할 필요가 없다.
세부 항목 나눠서 적기
- for num in range(len(data_list)) 반복
- swap = 0 (교환이 되었는지를 확인하는 변수를 두자)
- 반복문 안에서, for index in range(len(data_list) - num - 1) n - 1번 반복해야 하므로
- 반복문 안의 반복문에서, if data_list[index] > data_list[index + 1]이면
- data_list[index], data_list[index + 1] = data_list[index + 1], data_list[index]
- swap += 1
- 반복문 안에서, if swap == 0이면, break 끝
코드 작성
def bubblesort(data):
for index in range(len(data) - 1):
swap = False
for index2 in range(len(data) - index - 1):
if data[index2] > data[index2 + 1]:
data[index2], data[index2 + 1] = data[index2 + 1], data[index2]
swqp = True
if swap == False:
break
return data
improt random
data_list = random.sample(range(100), 50)
print(bubblesort(data_list))
시간복잡도 분석
- 반복문이 두 개 O( 𝑛2 )
- 최악의 경우, 𝑛(𝑛−1) / 2
- 완전 정렬이 되어 있는 상태라면 최선은 O(n)
기본정렬-삽입정렬
간단한 경우부터 복잡한 경우 순서대로 생각
- 예: data_list = [9, 3, 2, 5]
- 처음 한번 실행하면, key값은 9, 인덱스(0) - 1 은 0보다 작으므로 끝: [9, 3, 2, 5]
- 두 번째 실행하면, key값은 3, 9보다 3이 작으므로 자리 바꾸고, 끝: [3, 9, 2, 5]
- 세 번째 실행하면, key값은 2, 9보다 2가 작으므로 자리 바꾸고, 다시 3보다 2가 작으므로 끝: [2, 3, 9, 5]
- 네 번째 실행하면, key값은 5, 9보다 5이 작으므로 자리 바꾸고, 3보다는 5가 크므로 끝: [2, 3, 5, 9]
세부 항목 나눠서 적기
- for stand in range(len(data_list)) 로 반복
- key = data_list[stand]
- for num in range(stand, 0, -1) 반복
- 내부 반복문 안에서 data_list[stand] < data_list[num - 1] 이면,
- data_list[num - 1], data_list[num] = data_list[num], data_list[num - 1]
- 내부 반복문 안에서 data_list[stand] < data_list[num - 1] 이면,
코드 작성
def insertion_sort(data):
for index in range(len(data) - 1):
for index2 in range(index + 1, 0, -1):
if data[index2] < data[index2 - 1]:
data[index2], data[index2 - 1] = data[index2 - 1], data[index2]
else:
break
return data
import random
data_list = random.sample(range(100), 50)
print (insertion_sort(data_list))
시간복잡도 분석
- 반복문이 두 개 O( 𝑛2 )
- 최악의 경우, 𝑛∗(𝑛−1) / 2
- 완전 정렬이 되어 있는 상태라면 최선은 O(n)
기본정렬-선택정렬 (최솟값)
선택정렬이란? - 최솟값을 선택한다
- 주어진 데이터 중 최솟값을 찾아서 맨 앞에 위치한 값과 교체
- 맨 앞의 위치한 값을 뺀 나미저 데이터를 동일한 방법으로 반복
- 그림으로 보기1
- 그림으로 보기2 - selection_sort 선택
간단한 경우부터 복잡한 경우 순서대로 생각
- 데이터가 두 개 일때
- 예: dataList = [9, 1]
- data_list[0] > data_list[1] 이므로 data_list[0] 값과 data_ list[1] 값을 교환
- 예: dataList = [9, 1]
- 데이터가 세 개 일때
- 예: data_list = [9, 1, 7]
- 처음 한번 실행하면, 1, 9, 7 이 됨
- 두 번째 실행하면, 1, 7, 9 가 됨
- 예: data_list = [9, 1, 7]
- 데이터가 네 개 일때
- 예: data_list = [9, 3, 2, 1]
- 처음 한번 실행하면, 1, 3, 2, 9 가 됨
- 두 번째 실행하면, 1, 2, 3, 9 가 됨
- 세 번째 실행하면, 변화 없음
- 예: data_list = [9, 3, 2, 1]
세부 항목 나눠서 적기
- for stand in range(len(data_list) - 1) 로 반복
- lowest = stand 로 놓고,
- for num in range(stand, len(data_list)) stand 이후부터 반복
- 내부 반복문 안에서 data_list[lowest] > data_list[num] 이면,
- lowest = num
- data_list[num], data_list[lowest] = data_list[lowest], data_list[num]
코드 구현
def selection_sort(data):
for stand in range(len(data) - 1): # 2중 for문
lowest = stand
for index in range(stand + 1, len(data)):
if data[lowest] > data[index]:
lowest = index
data[lowest], data[stand] = data[stand], data[lowest]
return data
import random
data_list = random.sample(range(100), 10) # 0~99까지 랜덤수를 10개 생성
selection_sort(data_list)
-> [9, 12, 13, 24, 53, 55, 69, 80, 87, 98]
시간 복잡도 분석
반복문이 두 개 O( 𝑛2 )
실제로 상세하게 계산하면, 𝑛∗(𝑛−1) / 2
재귀
def factorial(num):
if num > 1:
return num * factorial(num - 1)
else:
return num
시간, 공간복잡도
- 시간 복잡도/공간 복잡도는 O(n-1) 이므로 결국, 둘 다 O(n)
- 일종의 n-1번 반복문을 호출한 것과 동일
- factorial() 함수를 호출할 때마다, 지역변수 n 이 생성됨
예제
- 재귀 함수를 활용해서 완성해서 1부터 num까지의 곱이 출력되게 만드세요
def multiple(num):
if num <= 1:
return num
return num * multiple(num - 1)
- 숫자가 들어 있는 리스트가 주어졌을 때, 리스트의 합을 리턴하는 함수를 만드세요
import random
data = random.sample(range(100), 10)
print(data)
def sum_list(data):
if len(data) <= 1:
return data[0]
return data[0] + sum_list(data[1:])
print(sum_list(data))
회문(palindrome)
- 회문(palindrome)은 순서를 거꾸로 읽어도 제대로 읽은 것과 같은 단어와 문장을 의미함
def palindrome(string):
if len(strung) <= 1: # 가운데 있는 회문 중간 글자까지 왔다는 것을 의미하므로
return True
if string[0] == string[-1]:
return palindrome(string[1:-1])
else:
return False
- 재귀 안 쓰고 간단하게 회문 판별
word = input('단어를 입력하세요: ')
print(word == word[::-1])
문제
1, 정수 n에 대해
- n이 홀수이면 3 X n + 1 을 하고,
- n이 짝수이면 n 을 2로 나눕니다.
- 이렇게 계속 진행해서 n 이 결국 1이 될 때까지 2와 3의 과정을 반복합니다.
예를 들어 n에 3을 넣으면,
` 3 10 5 16 8 4 2 1 `
이렇게 정수 n을 입력받아, 위 알고리즘에 의해 1이 되는 과정을 모두 출력하는 함수를 작성하세요.
def func(n):
print (n)
if n == 1:
return n
if n % 2 == 1:
return (func((3 * n) + 1))
else:
return (func(int(n / 2)))
동적 계획법 (Dynamic Programming)과 분할 정복 (Divide and Conquer)
정의
동적계획법 (DP 라고 많이 부름)
- 입력 크기가 작은 부분 문제들을 해결한 후, 해당 부분 문제의 해를 활용해서, 보다 큰 크기의 부분 문제를 해결, 최종적으로 전체 문제를 해결하는 알고리즘
- 상향식 접근법으로, 가장 최하위 해답을 구한 후, 이를 저장하고, 해당 결과값을 이용해서 상위 문제를 풀어가는 방식
- Memoization 기법을 사용함
- Memoization (메모이제이션) 이란: 프로그램 실행 시 이전에 계산한 값을 저장하여, 다시 계산하지 않도록 하여 전체 실행 속도를 빠르게 하는 기술
- 문제를 잘게 쪼갤 때, 부분 문제는 중복되어, 재활용됨
- 예: 피보나치 수열
분할 정복
- 문제를 나눌 수 없을 때까지 나누어서 각각을 풀면서 다시 합병하여 문제의 답을 얻는 알고리즘
- 하향식 접근법으로, 상위의 해답을 구하기 위해, 아래로 내려가면서 하위의 해답을 구하는 방식
- 일반적으로 재귀함수로 구현
- 문제를 잘게 쪼갤 때, 부분 문제는 서로 중복되지 않음
- 예: 병합 정렬, 퀵 정렬 등
공통점과 차이점
- 공통점
- 문제를 잘게 쪼개서, 가장 작은 단위로 분할
- 차이점
- 동적 계획법
- 부분 문제는 중복되어, 상위 문제 해결 시 재활용됨
- Memoization 기법 사용 (부분 문제의 해답을 저장해서 재활용하는 최적화 기법으로 사용)
- 분할 정복
- 부분 문제는 서로 중복되지 않음
- Memoization 기법 사용 안함
- 동적 계획법
동적계획법 예시
def fibo(num):
if num <= 1:
return num
return fibo(num - 1) + fibo(num - 2)
def fibo_dp(num):
cache = [ 0 for index in range(num + 1)]
cache[0] = 0 # 1보다 같거나 작으면 num 리턴 조건
cache[1] = 1
for index in range(2, num + 1):
cache[index] = cache[index - 1] + cache[index - 2] # 캐시로 저장한 숫자 재활용
return cache[num]
퀵 정렬 (quick sort)
- 기준점(pivot 이라고 부름)을 정해서, 기준점보다 작은 데이터는 왼쪽(left), 큰 데이터는 오른쪽(right) 으로 모으는 함수를 작성함
- 각 왼쪽(left), 오른쪽(right)은 재귀용법을 사용해서 다시 동일 함수를 호출하여 위 작업을 반복함
- 함수는 왼쪽(left) + 기준점(pivot) + 오른쪽(right) 을 리턴함
코드
def qsort(data):
if len(data) <= 1:
return data
pivot = data[0]
left = [ item for item in data[1:] if pivot > item ]
right = [ item for item in data[1:] if pivot <= item ]
return qsort(left) + [pivot] + qsort(right)
시간복잡도
- 병합정렬과 유사, 시간복잡도는 O(n log n)
- 단, 최악의 경우
- 맨 처음 pivot이 가장 크거나, 가장 작으면 모든 데이터를 비교하는 상황이 나옴
- O( 𝑛2 )
병합 정렬(merge sort)
설명
- 재귀용법을 활용한 정렬 알고리즘
- 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눈다.
- 각 부분 리스트를 재귀적으로 합병 정렬을 이용해 정렬한다.
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병한다.
- 참조-위키피디아
알고리즘
- mergesplit 함수 만들기
- 만약 리스트 갯수가 한개이면 해당 값 리턴
- 그렇지 않으면, 리스트를 앞뒤, 두 개로 나누기
- left = mergesplit(앞)
- right = mergesplit(뒤)
- merge(left, right)
- merge 함수 만들기
- 리스트 변수 하나 만들기 (sorted)
- left_index, right_index = 0
- while left_index < len(left) or right_index < len(right):
- 만약 left_index 나 right_index 가 이미 left 또는 right 리스트를 다 순회했다면, 그 반대쪽 데이터를 그대로 넣고, 해당 인덱스 1 증가
- if left[left_index] < right[right_index]:
- sorted.append(left[left_index])
- left_index += 1
- else:
- sorted.append(right[right_index])
- right_index += 1
코드
def merge(left, right):
merged = list()
left_index, right_index = 0, 0
# case1 - left/right 둘 다 있을 때
while len(left) > left_index and len(right) > right_index:
if left[left_lndex] > right[right_index]:
merged.append(right[right_index]) # 더 적은 수를 merged에
right_index += 1
else:
merged.append(left[left_index])
left_index += 1
# case2 - left만 남아 있을 때
while len(left) > left_index:
merged.append(left[left_index])
left_index += 1
# case3 - right만 남아 있을 때
while len(right) > right_index:
merged.append(right[right_index])
right_index += 1
return merged
def mergesplit(data):
if len(data) <= 1:
return data
medium = int(len(data) / 2)
left = mergesplit(data[:medium])
right = mergesplit(data[medium:])
return merge(left, right)
import random
data_list = random.sample(range(100), 10)
mergesplit(data_list)
시간복잡도
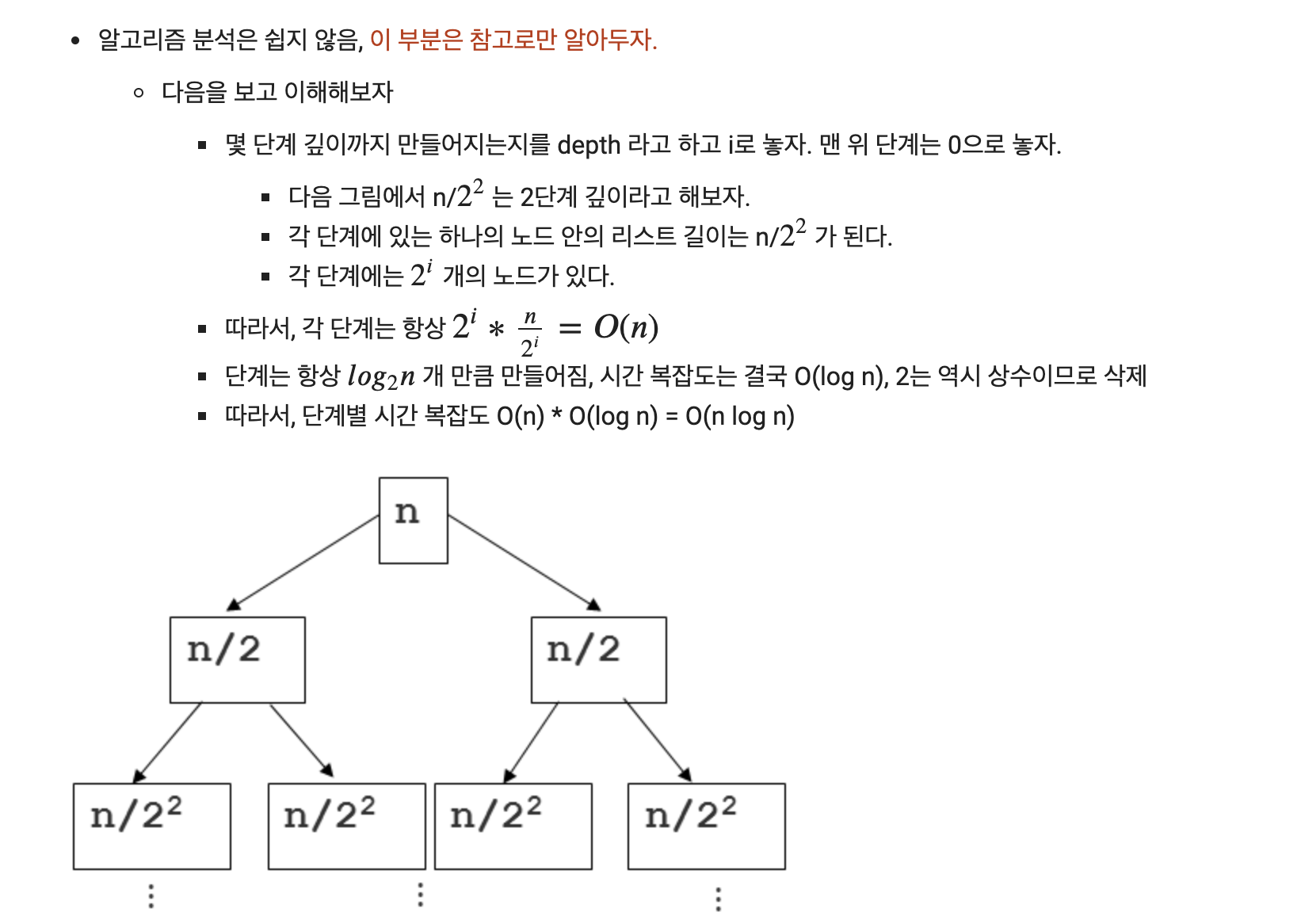
그래프 이해
그래프 (Graph) 관련 용어
- 노드 (Node): 위치를 말함, 정점(Vertex)라고도 함
- 간선 (Edge): 위치 간의 관계를 표시한 선으로 노드를 연결한 선이라고 보면 됨 (link 또는 branch 라고도 함)
- 인접 정점 (Adjacent Vertex) : 간선으로 직접 연결된 정점(또는 노드)
- 참고 용어
- 정점의 차수(Degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 진입 차수(In-Degree): 방향 그래프에서 외부에서 오는 간선의 수
- 진출 차수(Out-Degree): 방향 그래프에서 외부로 향하는 간선의 수
- 경로 길이(Path Length): 경로를 구성하기 위해 사용된 간선의 수
- 단순 경로 Simple Path): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
- 사이클(Cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우
그래프 (Graph) 종류
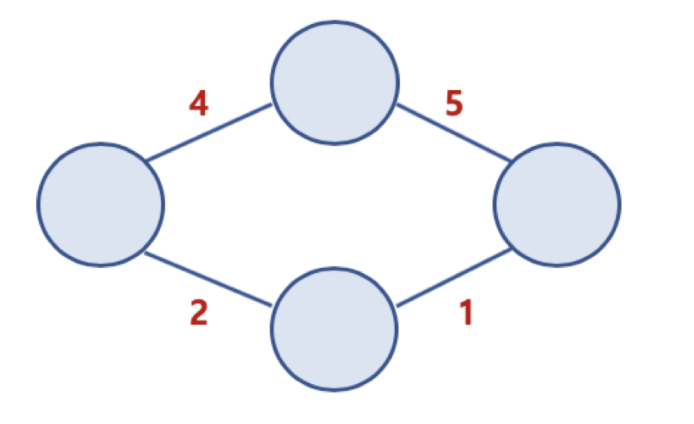
- 가중치 그래프 (Weighted Graph) 또는 네트워크 (Network)
- 간선에 비용 또는 가중치가 할당된 그래프
- 연결 그래프 (Connected Graph) 와 비연결 그래프 (Disconnected Graph)
- 연결 그래프 (Connected Graph)
- 무방향 그래프에 있는 모든 노드에 대해 항상 경로가 존재하는 경우
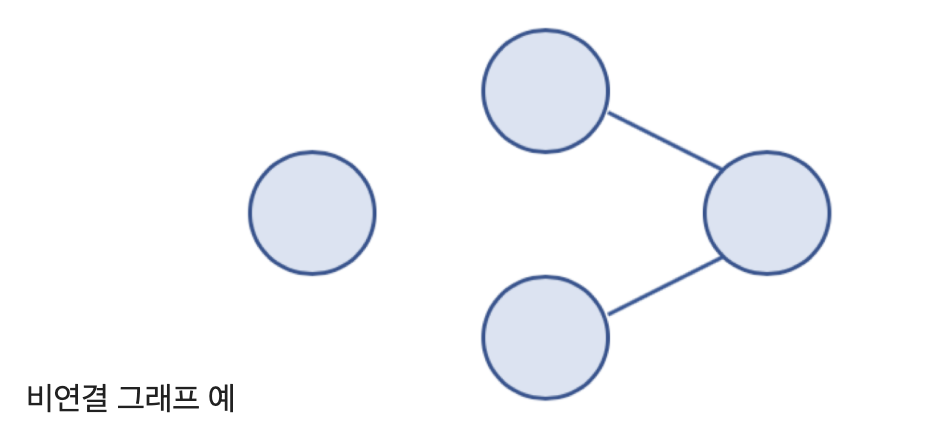
- 비연결 그래프 (Disconnected Graph)
- 무방향 그래프에서 특정 노드에 대해 경로가 존재하지 않는 경우
- 연결 그래프 (Connected Graph)
- 사이클 (Cycle) 과 비순환 그래프 (Acyclic Graph)
- 사이클 (Cycle)
- 단순 경로의 시작 노드와 종료 노드가 동일한 경우
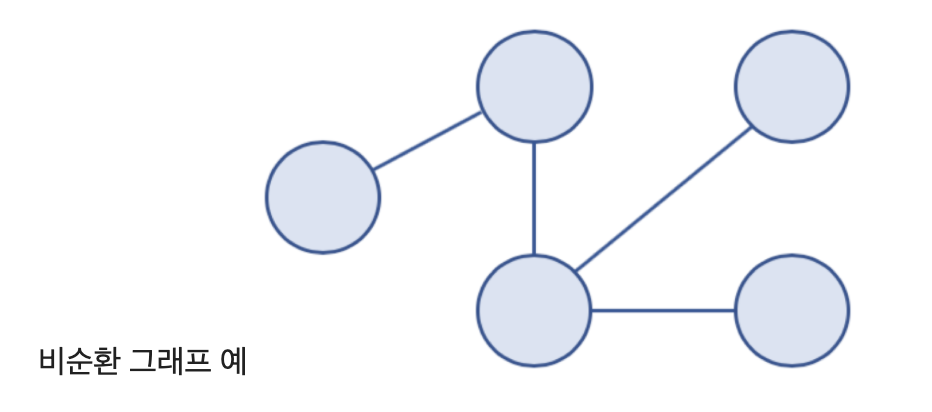
- 비순환 그래프 (Acyclic Graph)
- 사이클이 없는 그래프
- 사이클 (Cycle)
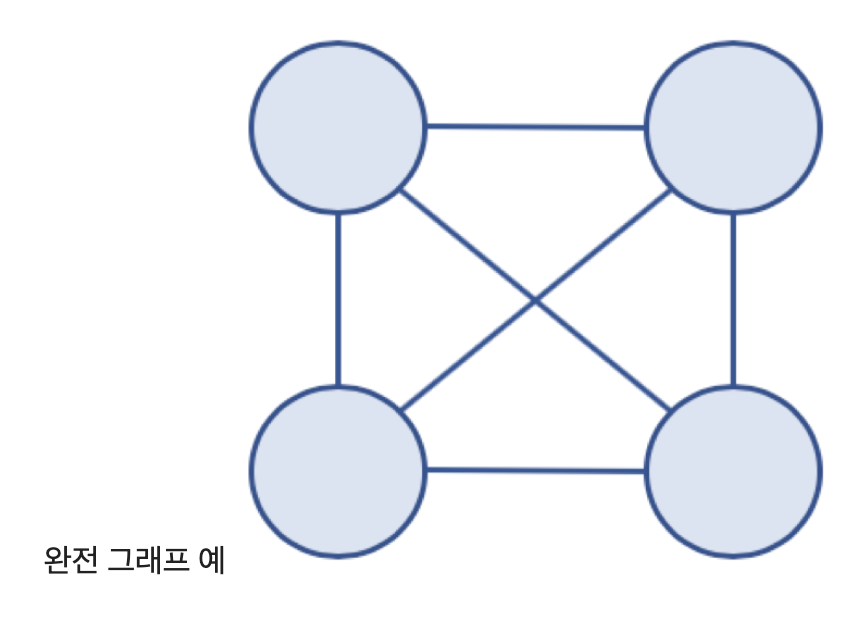
- 완전 그래프 (Complete Graph)
- 그래프의 모든 노드가 서로 연결되어 있는 그래프
그래프와 트리의 차이
- 트리는 그래프에 속한 종류라고 볼 수 있음

그래프 알고리즘
깊이 우선 탐색 (Depth-First Search)
BFS 와 DFS 란?
- 대표적인 그래프 탐색 알고리즘
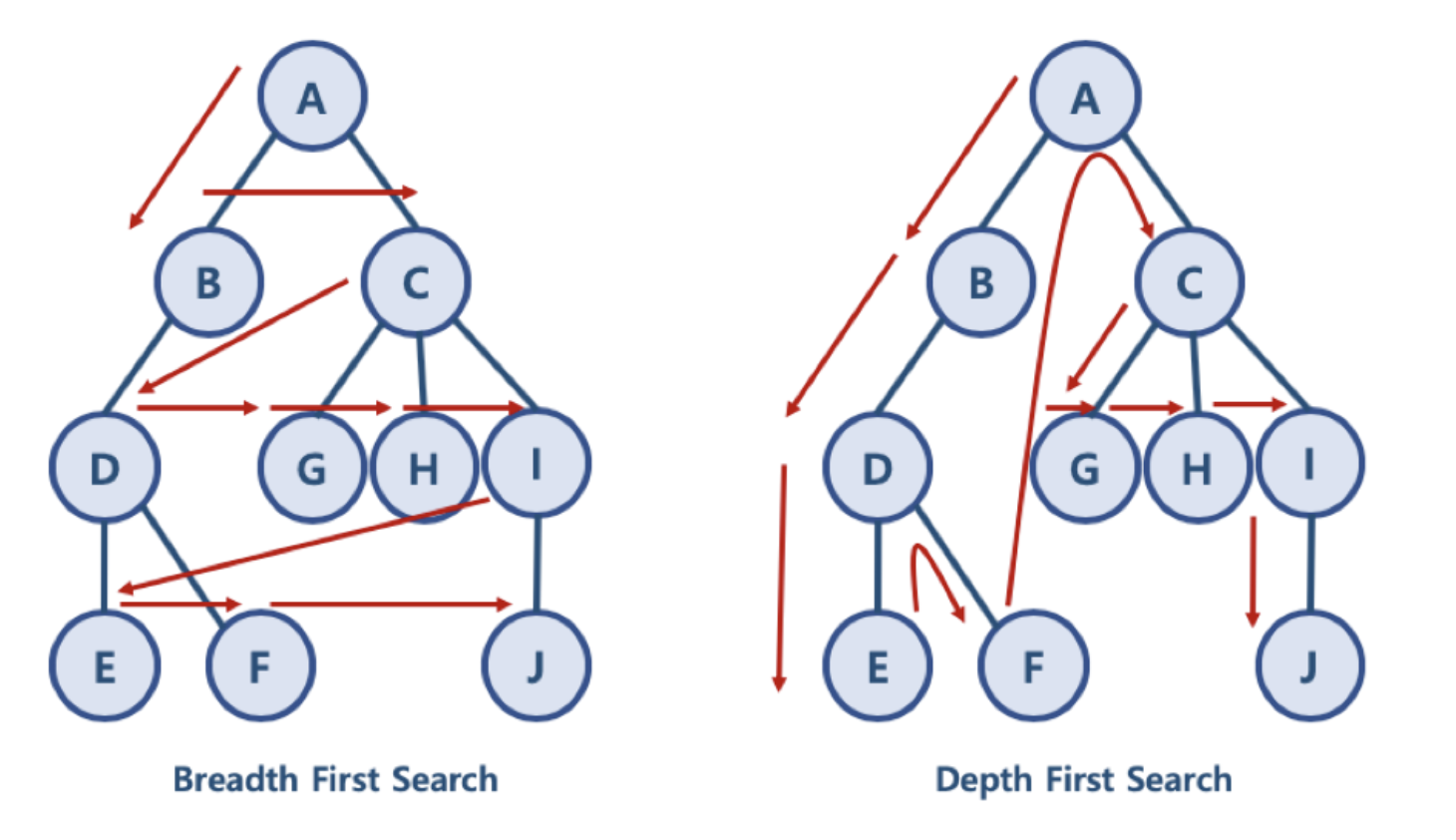
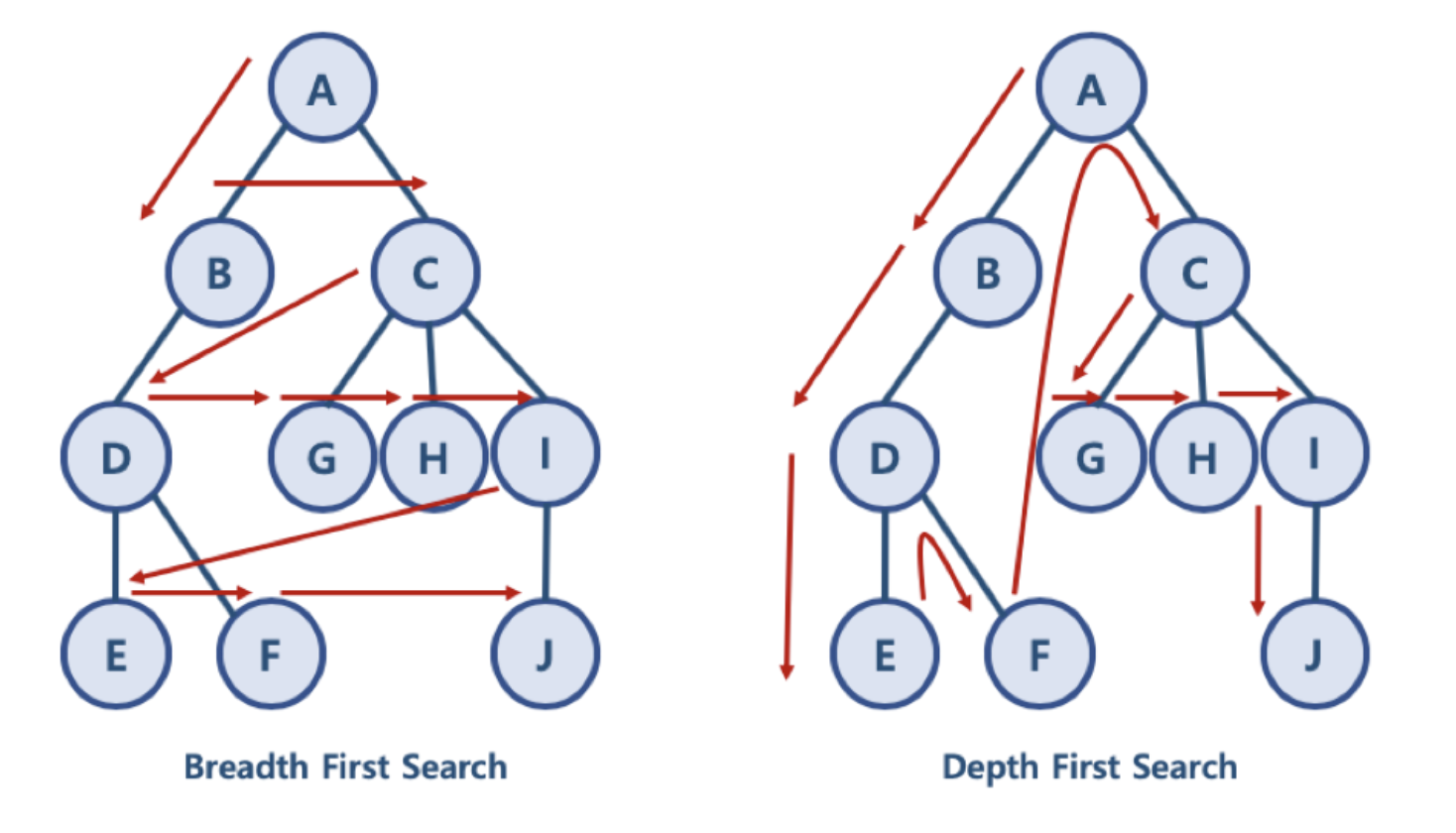
- 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
- 깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식
- BFS/DFS 방식 이해를 위한 예제
- BFS 방식: A - B - C - D - G - H - I - E - F - J
- 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
- DFS 방식: A - B - D - E - F - C - G - H - I - J
- 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함
- BFS 방식: A - B - C - D - G - H - I - E - F - J
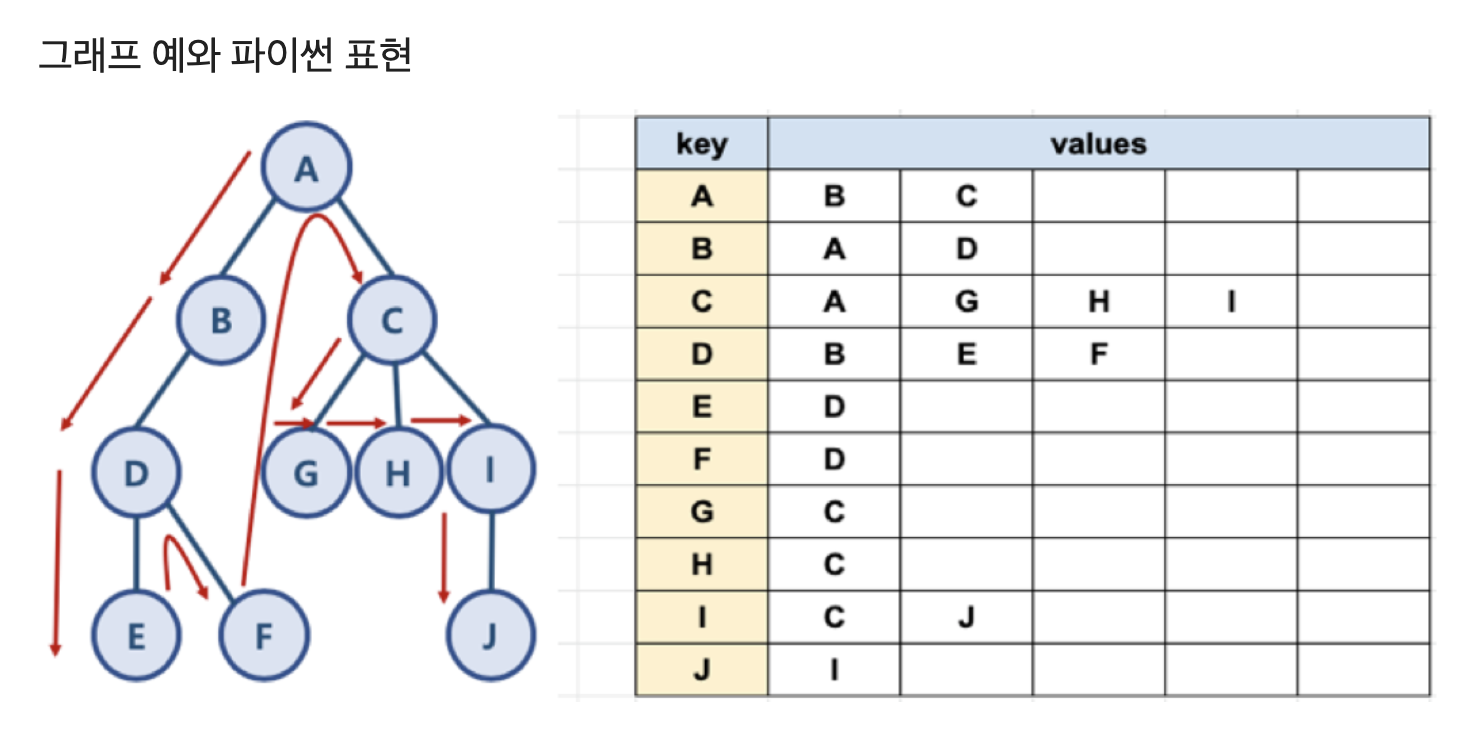
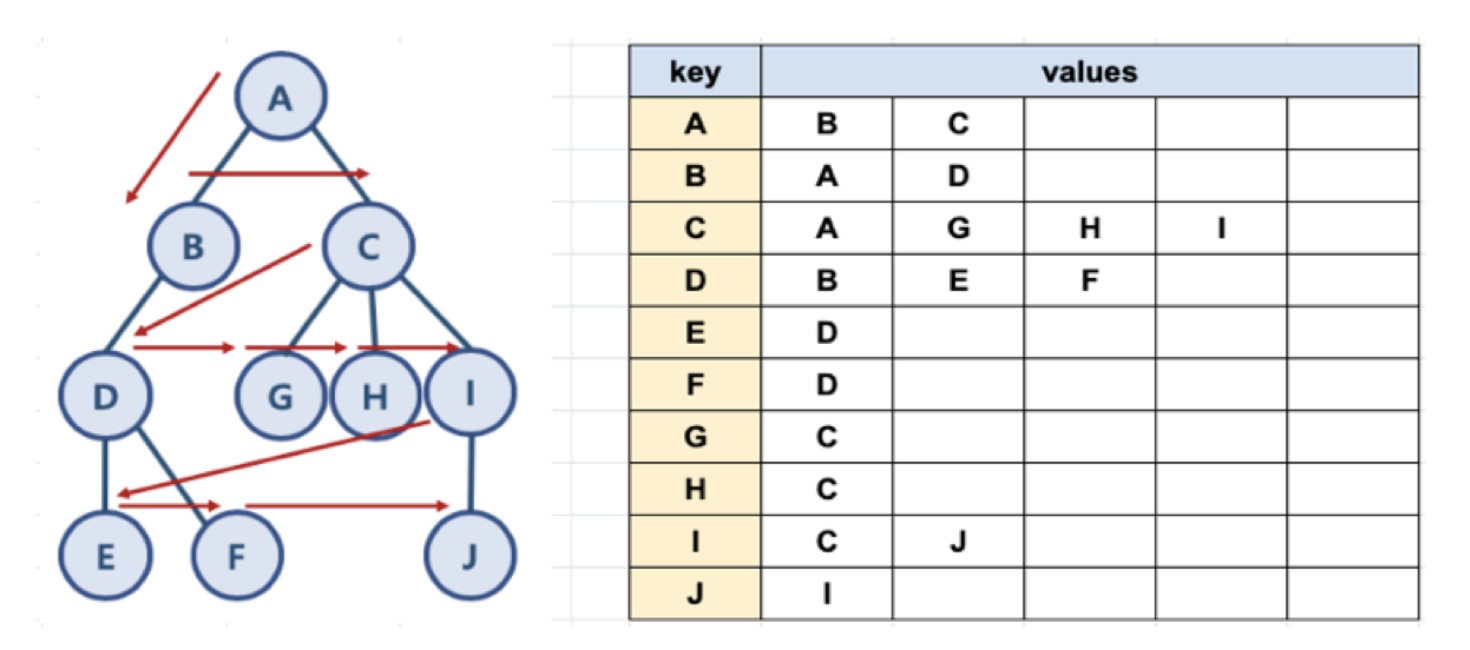
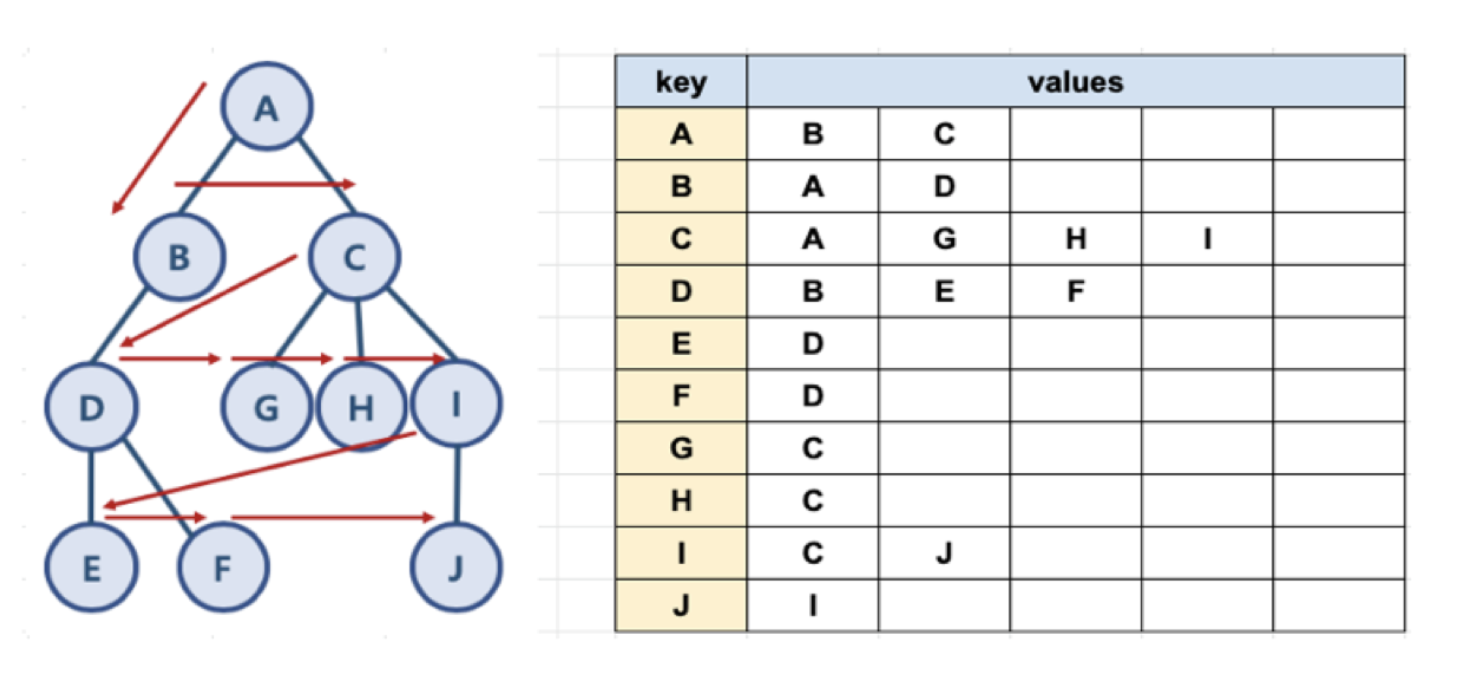
파이썬으로 그래프를 표현하는 방법
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
DFS 알고리즘 구현
- 자료구조 스택과 큐를 활용함
- need_visit 스택과 visited 큐, 두 개의 자료 구조를 생성
- BFS 자료구조는 두 개의 큐를 활용하는데 반해, DFS 는 스택과 큐를 활용한다는 차이가 있음을 인지해야 함
def dfs(graph, start_node):
visited, need_visit = list(), list()
need_visit.append(start_node)
while need_visit:
node = need_visit.pop()
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
return visited
dfs(graph, 'A')
시간 복잡도
- 일반적인 DFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
- 시간 복잡도: O(V + E)
너비 우선 탐색 (Breadth-First Search)
BFS/DFS 방식 이해를 위한 예제
- BFS 방식: A - B - C - D - G - H - I - E - F - J
- 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
- DFS 방식: A - B - D - E - F - C - G - H - I - J
- 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함
파이썬으로 그래프를 표현하는 방법
graph = dict()
graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']
BFS 알고리즘 구현
- 자료구조 큐를 활용함
- need_visit 큐와 visited 큐, 두 개의 큐를 생성
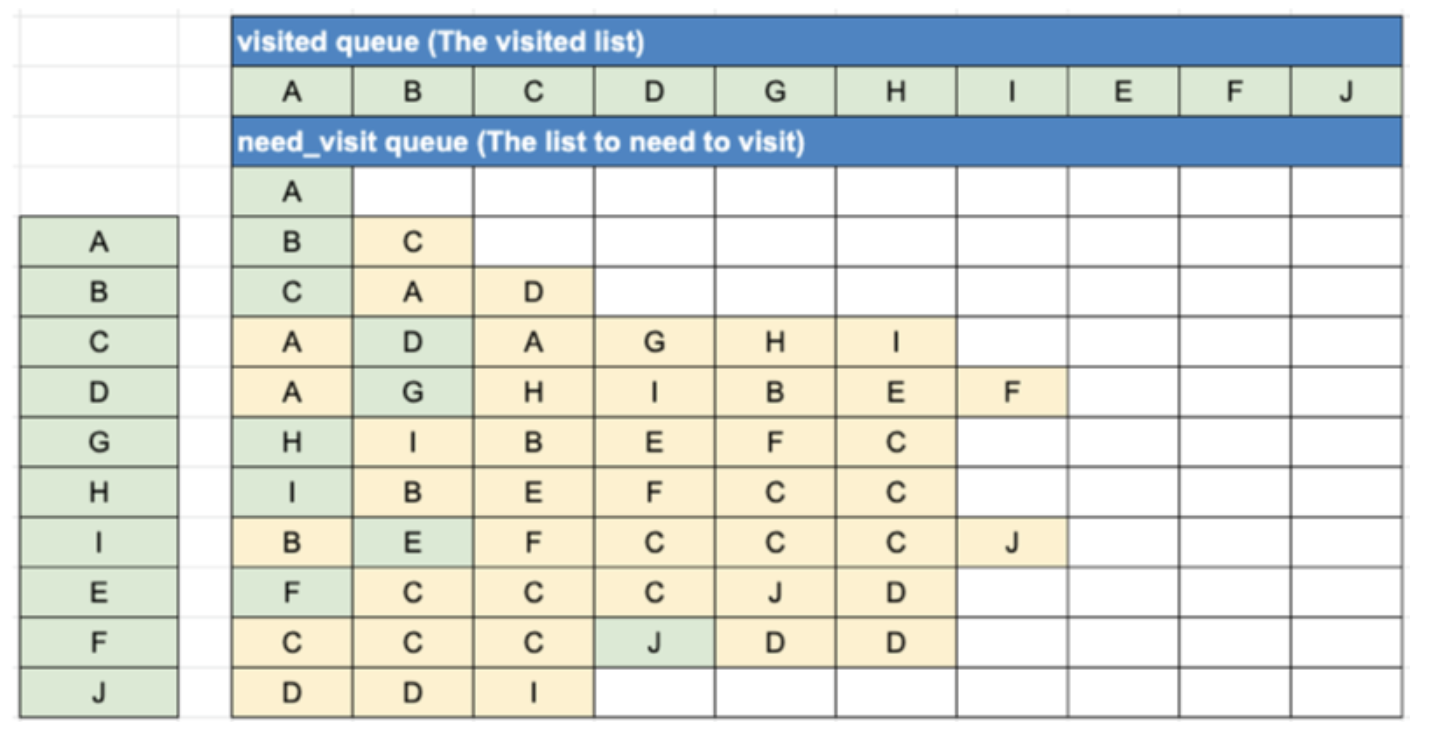
def bfs(graph, start_node):
visited = list()
need_visit = list()
need_visit.append(start_node)
while need_visit:
node = need_visit.pop(0)
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
return visited
bfs(graph, 'A')
시간 복잡도
- 일반적인 BFS 시간 복잡도
- 노드 수: V
- 간선 수: E
- 위 코드에서 while need_visit 은 V + E 번 만큼 수행함
- 시간 복잡도: O(V + E)
def bfs(graph, start_node):
visited = list()
need_visit = list()
need_visit.append(start_node)
count = 0
while need_visit:
count += 1
node = need_visit.pop(0)
if node not in visited:
visited.append(node)
need_visit.extend(graph[node])
print (count)
return visited